【浅水流方程式】サイトマップ(ここから関連記事が探せます)
1次元浅水流方程式(Shallow Water Equation, SWE)の導出(勾配と摩擦なし)をします。取りあえず導出すべき1次元浅水流方程式の基本形を書いておきます。要は慣れです。慣れると怖くなくなります。
水平な長方形の一様断面を考えることにします。今回は勾配と摩擦は無しにしましょう。浅水流方程式においては非圧縮性が仮定されています(密度が時間・場所変化しない)。まず、水深と流速で記述した場合は
となります。ここで は時間、
は1次元座標、
は水深、
は流速、
は重力加速度です。上の式が連続式で、下の式が運動量方程式です。次に水深と流量を用いて記述する場合です。水深と流量の関係
を用いて上式を変形すると
となります。こちらもどうぞ。
さて変数は以下の図のように配置されているとします。
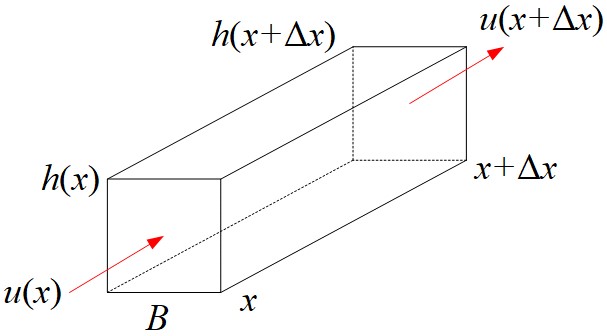
手前から奥へ向けて( 方向へ)水が流れています。各地点の流速
と水深
が与えられています。また、水路の幅は
とします。一様断面なので
が一定であることに注意してください。区間
を考えます。
まず連続式からいきましょう。要するにこの式は質量保存則をあらわしています。区間 における質量の保存を考えます。保存則は
単位時間あたりに入ってくる量 - 単位時間あたりに出ていく量
という関係式から導かれます。物理においてはだいたいこのパターンなのでよく覚えておいてください。まず、区間 における質量の時間変化は、水の密度を
として(非圧縮性を仮定しているので定数扱い)
と書けます。次に から単位時間あたりに入ってくる質量は
であり、 から単位時間あたりに出ていく質量は
と書けます。これは において以下の図のような水の塊が流れ込んでくるからです。
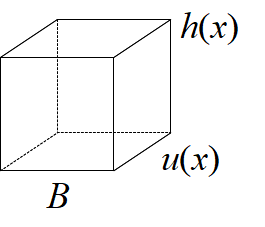
高さが で、
方向の奥行が
の水の塊です。
方向の奥行が
になるのは、単位時間で考えているからです。流速 (m/s) × 1 (s) = 距離 (m) のようになっています。
からは高さが
で、
方向の奥行が
の水の塊が出ていきます。さて、これで保存則の要素が揃いました。関係式に代入すると
となります。定数である で両辺を割ってから右辺を左辺に移項し、
で割ると
を得ます。 の極限をとると、微分の定義より
が得られます。これが連続式です!
次に運動量方程式を導出します。運動量方程式は運動量保存則のことです。
区間 における質量の保存を考えます。
参考
E. F. Toro, Shock-Capturing Methods for Free-Surface Shallow Flows, 第2章
R. J. Leveque, Finite Volume Methods for Hyperbolic Problems, 第13章
R. Szymkiewicz, Numerical Modeling in Open Channel Hydraulics, 第1章

Shock-Capturing Methods for Free-Surface Shallow Flows
- 作者: Eleuterio F. Toro
- 出版社/メーカー: Wiley
- 発売日: 2001/03/23
- メディア: ハードカバー
- この商品を含むブログを見る

Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics)
- 作者: Randall J. Leveque
- 出版社/メーカー: Cambridge University Press
- 発売日: 2002/08/29
- メディア: ペーパーバック
- この商品を含むブログを見る

- 作者: Romuald Szymkiewicz
- 出版社/メーカー: Springer
- 発売日: 2010/03/10
- メディア: Kindle版
- この商品を含むブログを見る