数学とか語学とか楽しいよね

フランス語、ドイツ語、ロシア語、アラビア語、オランダ語、英語、スペイン語、ラテン語とか数学とか数値計算（有限要素法、有限体積法、差分法、格子ボルツマン法、数理最適化、C++コード付き）とか勉強したことをまとめます。右のカテゴリーから興味のある記事を探してください。最近はクラシックの名演も紹介しています。Amazonアソシエイトを使用しています。

【有限体積法】2次元非構造有限体積法のコードを作ってみました　三次元図付き

数値流体力学数値計算有限体積法

2次元非構造有限体積法のコードを作ってみました。cell-centeredと呼ばれる方法を使っています。解く方程式は2次元の定常移流拡散方程式です。流れ場はx方向が $u=x$ 、y方向が $v=-y$ と与えます。領域は $(0,1)^2$ で、境界条件は

・ $x=0$ においてDirichlet条件 $\phi=1-y$
・ $y=1$ においてDirichlet条件 $\phi=0$
・ $y=0$ においてNeumann条件 $\frac{\partial \phi}{\partial y} = 0$
・ $x=1$ においてNeumann条件 $\frac{\partial \phi}{\partial x} = 0$

です。ファーツィガーの『コンピュータによる流体力学』4.7の計算例と同じ問題です。

コンピュータによる流体力学

コンピュータによる流体力学

作者: J.H.ファーツィガー,M.ペリッチ,小林敏雄
出版社/メーカー: 丸善出版
発売日: 2012/06/05
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

コードを作るうえで一番参考になった本は、やはりVersteegの『数値流体力学』です。非構造格子の話は第11章にあります。

数値流体力学第2版

数値流体力学第2版

作者: H.K.Versteeg,W.Malalasekera,松下洋介,齋藤泰洋,青木秀之,三浦隆利
出版社/メーカー: 森北出版
発売日: 2011/05/31
メディア: 単行本（ソフトカバー）
クリック: 4回
この商品を含むブログを見る

洋書も含めて非構造格子における有限体積法が詳しく説明されている本は本当に少なく、私も作るのに非常に苦労しました。Versteegの本は高いですが値段に見合う情報が載っています。しかも日本語で読めるのは有難いです。

メッシュはFreeFem++で作成したDelaunay（ドロネーまたはデローニー）三角形メッシュを拝借しています。FreeFem++は非常に扱いやすく、簡単に数値実験ができるのでおすすめです。試してみてください。

FreeFem++の紹介 - Qiita

f:id:mutsumunemitsutan:20190418234707p:plain:w500 — 計算に用いたメッシュ（非構造格子）

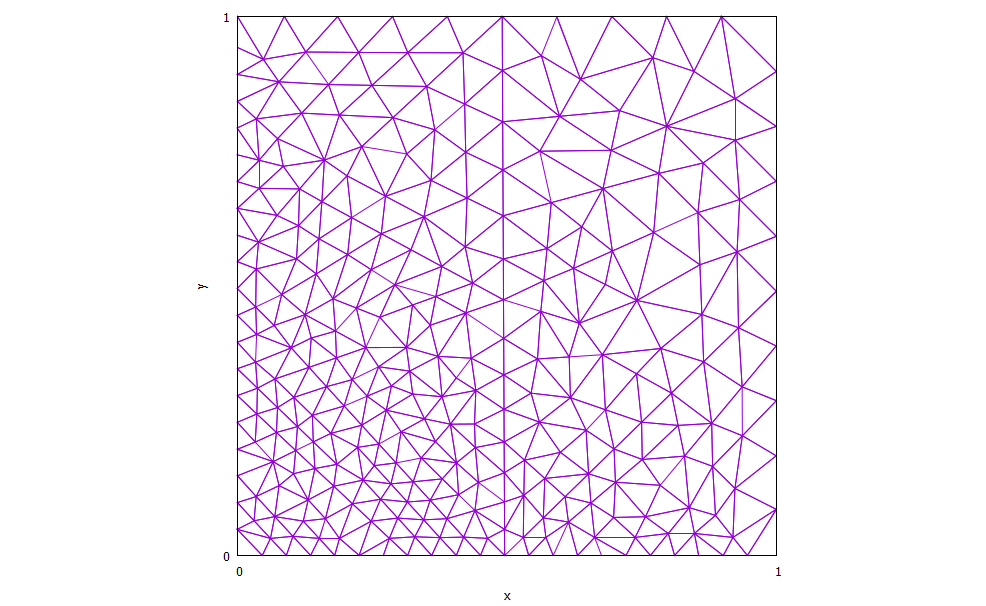
まずメッシュですが、節点数が291、セル数が518です。左下に多めに節点を集めています。

次に計算結果です。出力の都合上、隣接点を繋いでいます。また、境界上の点（境界条件）は出力していません。

f:id:mutsumunemitsutan:20190418182612p:plain:w500 — 非構造格子による計算結果

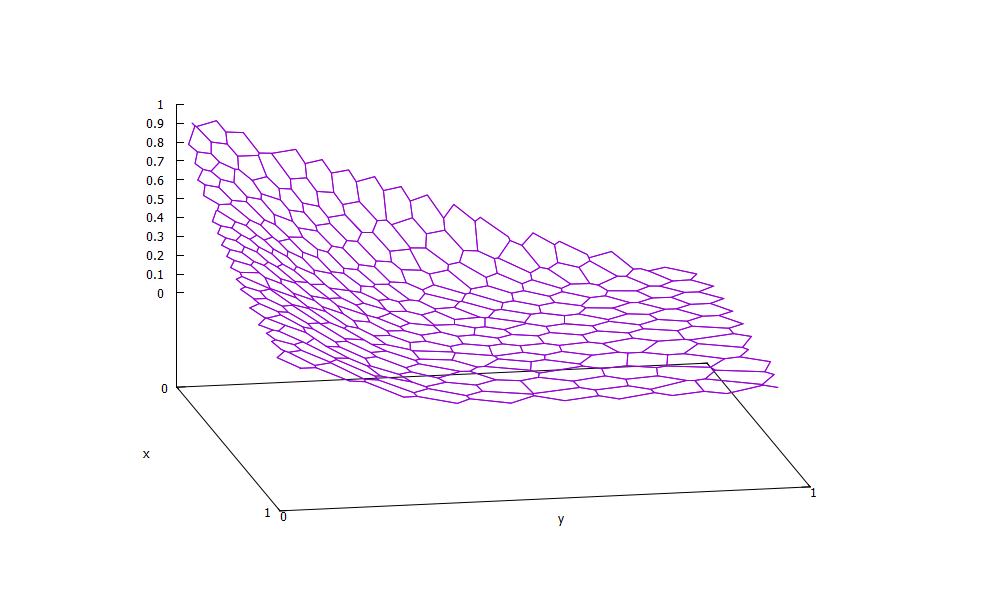
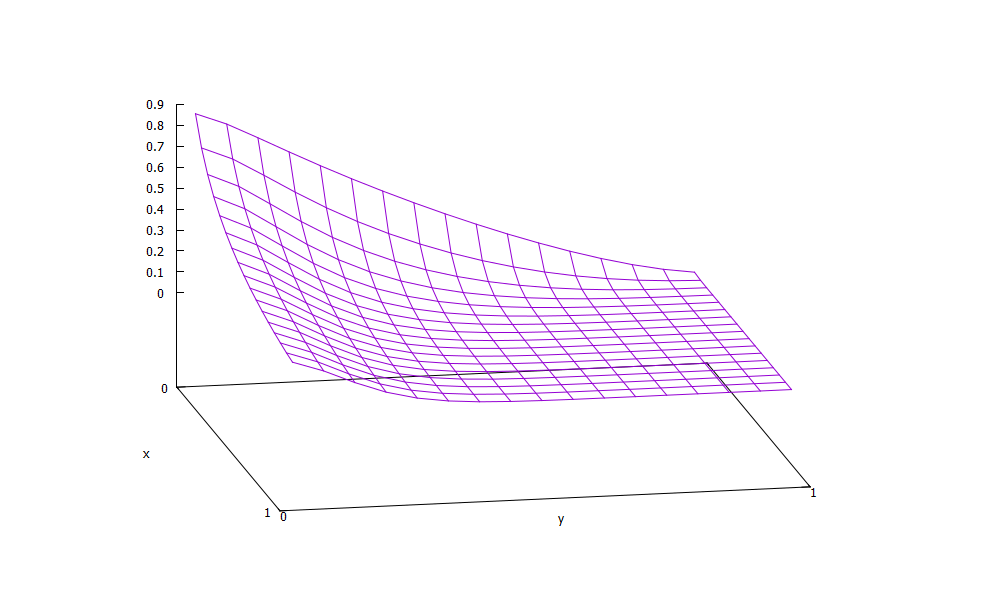
比較のために構造格子で解いた場合の結果も載せておきます。17×17=289節点、16×16=256セルです。

f:id:mutsumunemitsutan:20190418182536p:plain:w500 — 構造格子による計算結果

コードはもう少し整理してから公開します。