【有限体積法】Keller-Segel方程式を有限体積法で解く　C++コード付き

はじめに

今回はKeller-Segel方程式を有限体積法で解いていきます。半年前ぐらいに作ってどうも動かなくてしばらく放置していましたが、やっと動きました！！！Keller-Segel方程式とは粘菌の凝集をモデル化した非線型連立方程式です。走化性モデルとして有名です。

Keller-Segel方程式

Keller-Segel方程式とは粘菌の凝集をモデル化したもので、

$\displaystyle \begin{eqnarray} &u_t=-[F(u,v)]_x\\ &0=v_{xx}-\gamma v + \alpha u\\ &F(u,v)=-u_x+(\lambda v)_x u\\ \end{eqnarray}$

のような非線型連立方程式です。ここで、 $u=u(t,x)$ が粘菌の密度、 $v=v(t,x)$ が粘菌の放出する化学物質の濃度、 $F(u,v)$ はフラックス、 $\gamma$ 、 $\alpha$ 、 $\lambda$ は係数です。粘菌はランダムに広がりつつ、化学物質の濃度が高い方向に進もうとします。それぞれフラックスの1項目と2項目にあたります。特に、2項目を走化性（chemotaxis）と言います。考える領域を $(0,1)$ として、境界条件はノイマン条件（反射壁）

$\displaystyle \begin{eqnarray} &\left.F(u,v)\right|_{x=0,1}=0\\ &\left.v_x\right|_{x=0,1}=0 \end{eqnarray}$

とします。初期条件は $u$ と $v$ に適当な分布を与えます。

離散化

離散化は、以下の斉藤氏のものを採用しました。下記文献では詳細にスキームの数学解析がなされており非常にためになります。式で言うと(6)、(7)、(8)です。
https://www.jstage.jst.go.jp/article/bjsiam/19/4/19_KJ00005931649/_pdf

簡単にまとめますと、 $u$ の時間発展には $v^{n-1}$ を用いることによって線型化します。また、フラックスの項は、 $(\lambda v)_x$ を移流流速と考えて風上化をかけます。

また、『エンジニアのための有限要素法入門』のpp.173-191に、有限要素法によるKeller-Segel方程式の離散化が載っています。

エンジニアのための有限要素法入門―基礎から応用へ

作者:勉, 野原
発売日: 2016/05/01
メディア: 単行本

計算結果

ケース1

これは、初期時刻に粘菌の集団が2つある場合です。以下が計算結果です。青が粘菌の密度 $u$ です。

f:id:mutsumunemitsutan:20200428232046g:plain:w500

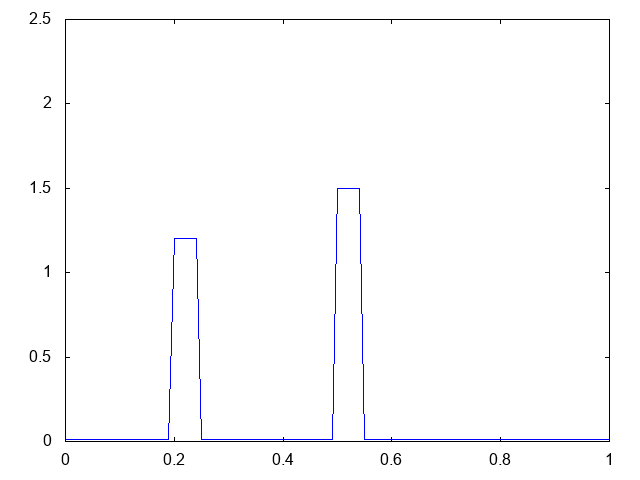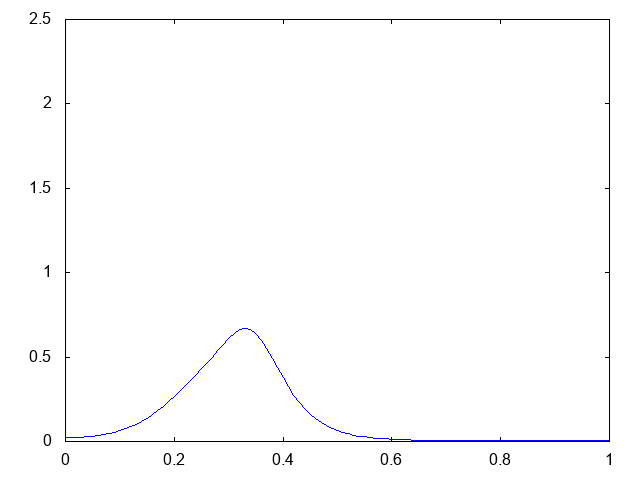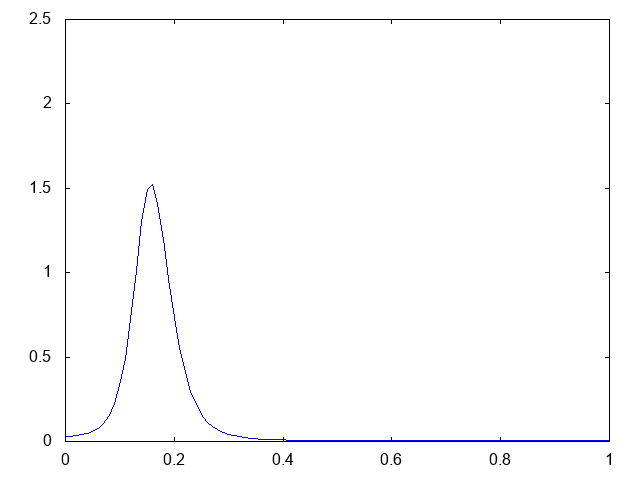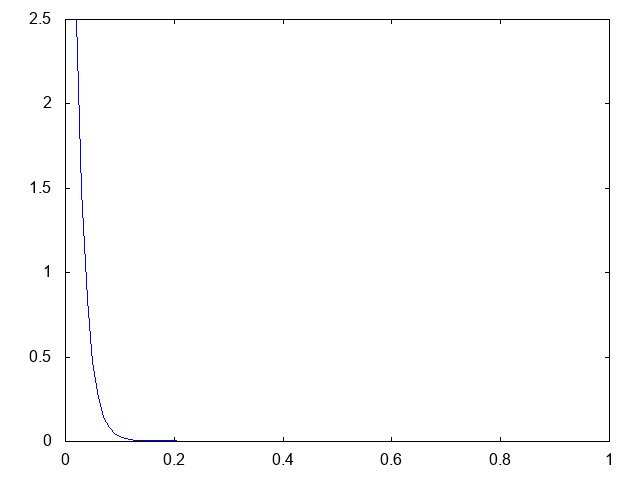
2つあった粘菌の集団が1つに合体し、左へと移動し、最終的に境界で爆発的に凝集していく様が観察できます。

ケース2

これも、初期時刻に粘菌の集団が2つある場合です。ただしケース1より少しだけ離して配置してあります。以下が計算結果です。

f:id:mutsumunemitsutan:20200428233114g:plain:w500

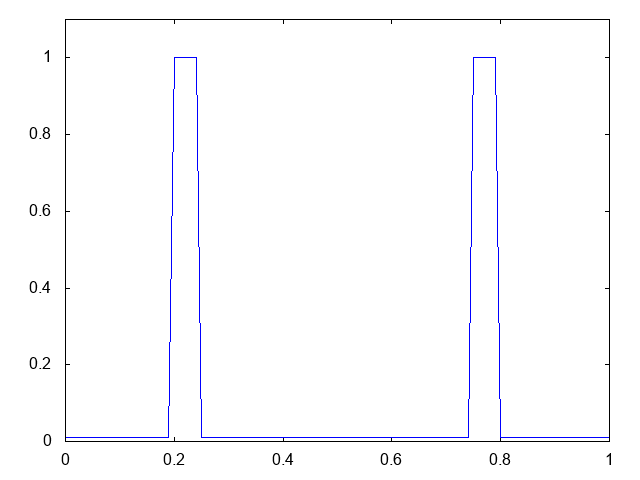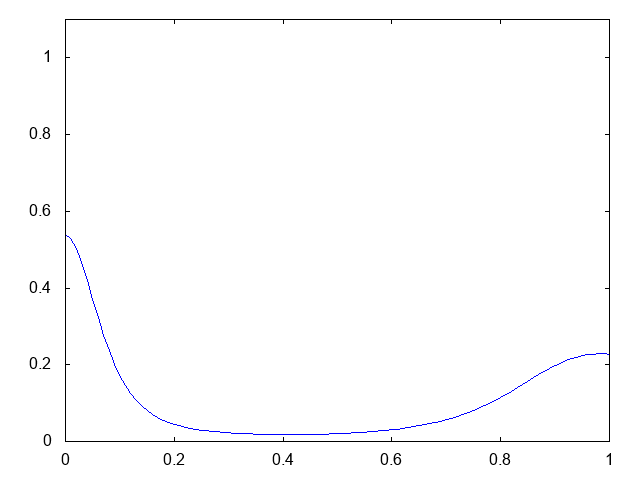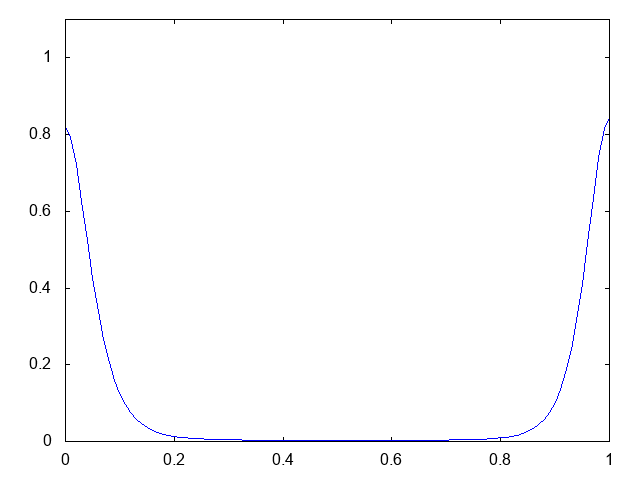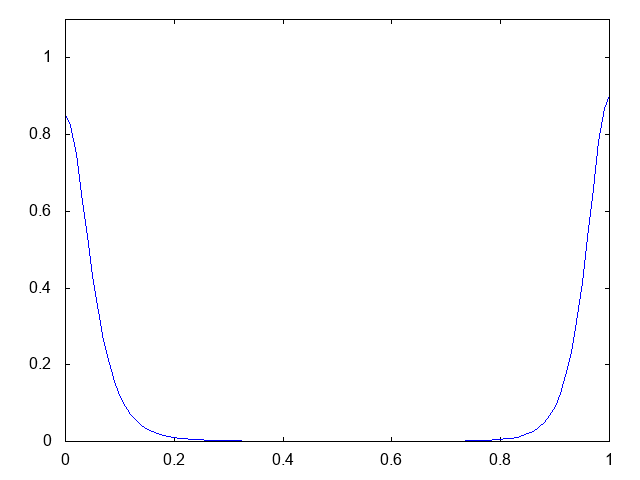
2つあった粘菌の集団がそれぞれ左右へと移動し、最終的に境界でそれぞれ爆発的に凝集していく様が観察できます。

C++コード

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <string>
#include <sstream>
#include <algorithm>

using namespace std;

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void output(double u[], int Node, double dx, double v[])
{
	stringstream ss;
	string name1,name2;
	ofstream f1,f2;
	static int count=0;
	
	ss<<count;
	name1=ss.str();
	name1="u_" + name1 + ".txt";
	name2=ss.str();
	name2="v_" + name2 + ".txt";
	f1.open(name1.c_str ());
	f2.open(name2.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		f1<<dx*double(i)<<" "<<u[i]<<endl;
		f2<<dx*double(i)<<" "<<v[i]<<endl;
	}
	f1<<endl;
	f2<<endl;
	
	count+=1;
}

int main()
{
	int i,j,k;
	int Cell=100;
	int Node=Cell+1;
	double LL=1.0;
	double dx=LL/Cell;
	double dt=0.000025;
	double NT=2000;
	double alpha=10.0;
	double lam=100.0;
	double gamma=5;
	double u[Node];
	double un[Node];
	double v[Node];
	double vn[Node];
	double b[Node];
	double AD[Node];
	double AL[Node];
	double AR[Node];
	double FR,FL;
	int div=5;
	double uhat;
	double bb;
	
	//initial condition//
	for(i=0;i<Node;i++)
	{
		double a=3*sin(4.0*atan(1.0)/LL*double(i)*dx);
		u[i]=0.01;
		v[i]=a;
	}

	for(i=20;i<25;i++)
	{
		u[i]=1.2;
	}

	for(i=50;i<55;i++)
	{
		u[i]=1.5;
	}

	output(u,Node,dx,v);
	
	for(k=1;k<=NT;k++)
	{
		//v//
		for(i=1;i<Node-1;i++)
		{
			uhat=(u[i]+u[i+1])/2.0;

			//diffusion//
			AL[i]=1.0/dx/dx;
			AD[i]=-2.0/dx/dx;
			AR[i]=1.0/dx/dx;

			//decomposition//
			AD[i]+=-gamma;

			//secretion//
			b[i]=-alpha*uhat;
		}
	
		//BC//
		//i=0//
		uhat=u[0];

		//diffusion//
		AD[0]=-2.0/dx/dx;
		AR[0]=2.0/dx/dx;

		//decomposition//
		AD[0]+=-gamma;

		//secretion//
		b[0]=-alpha*uhat;


		//i=Node-1//
		uhat=u[Node-1];

		//diffusion//
		AL[Node-1]=2.0/dx/dx;
		AD[Node-1]=-2.0/dx/dx;

		//decomposition//
		AD[Node-1]+=-gamma;

		//secretion//
		b[Node-1]=-alpha*uhat;

		//solve for v//
		tdma(AD,AL,AR,b,vn,Node);

		
		//u//
		for(i=1;i<Node-1;i++)
		{
			FR=-(u[i+1]-u[i])/dx;

			bb=lam*(vn[i+1]-vn[i])/dx;
			if(bb>=0) FR+=bb*u[i];
			else FR+=bb*u[i+1];

			FL=-(u[i]-u[i-1])/dx;
			bb=lam*(vn[i]-vn[i-1])/dx;
			if(bb>=0) FL+=bb*u[i-1];
			else FL+=bb*u[i];

			un[i]=u[i]-dt/dx*(FR-FL);
		}

		//BC//
		//i=0//
		FR=-(u[1]-u[0])/dx;
		bb=lam*(vn[1]-vn[0])/dx;
		if(bb>=0) FR+=bb*u[0];
		else FR+=bb*u[1];
		FL=0;
		un[0]=u[0]-dt/dx*(FR-FL);

		//i=Node-1//
		FR=0;
		FL=-(u[Node-1]-u[Node-2])/dx;
		bb=lam*(vn[Node-1]-vn[Node-2])/dx;
		if(bb>=0) FL+=bb*u[Node-2];
		else FL+=bb*u[Node-1];
		un[Node-1]=u[Node-1]-dt/dx*(FR-FL);

		//update//
		for(i=0;i<Node;i++)
		{
			v[i]=vn[i];
			u[i]=un[i];
		}
		
		if(k%div==0)
		{
			cout<<k<<endl;
			output(u,Node,dx,v);
		}
	}
	
	return 0;
}

おわりに

制御入れたらおもしろいのでは？