数学とか語学とか楽しいよね

フランス語、ドイツ語、ロシア語、アラビア語、オランダ語、英語、スペイン語、ラテン語とか数学とか数値計算（有限要素法、有限体積法、差分法、格子ボルツマン法、数理最適化、C++コード付き）とか勉強したことをまとめます。右のカテゴリーから興味のある記事を探してください。最近はクラシックの名演も紹介しています。Amazonアソシエイトを使用しています。

【有限体積法】1次元移流方程式をMUSCL法で解く　C++コード付き

数値計算 Navier-Stokes方程式 偏微分方程式 数値流体力学 有限体積法

今回は1次元移流方程式を1次の風上差分+MUSCL法で解いていきます。MUSCL法とは、セル内で一定だった未知数のプロファイルを1次以上の関数で補外しセル界面での値を計算し、その値を用いて数値流速を計算することによって高次精度を達成する方法です。その際に、数値振動が発生しないように勾配制限関数（slope limiter）が用いられます。今回はminmod関数を使いました。


1次元移流方程式とは

\displaystyle \frac{\partial u}{\partial t} + V\frac{\partial u}{\partial x} =0, \quad x \in [0, L]

のような一階の偏微分方程式のことをいいます。ここで、 u は溶質の濃度、 V は風などによる移流速度です。


今回の計算条件は、移流速度が正 V=0.1 で、初期条件は領域の左端の矩形波（長方形の波）です。比較のために普通の風上差分で解いた結果も載せます。


これが計算結果です。青がMUSCLで、赤が1次の風上差分です。

f:id:mutsumunemitsutan:20190706143305g:plain:w500

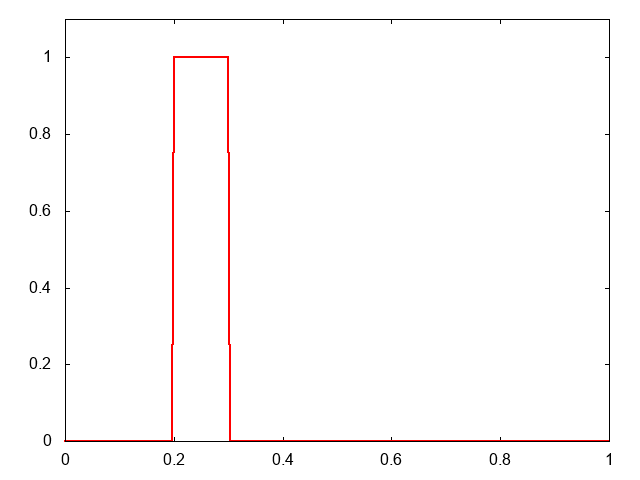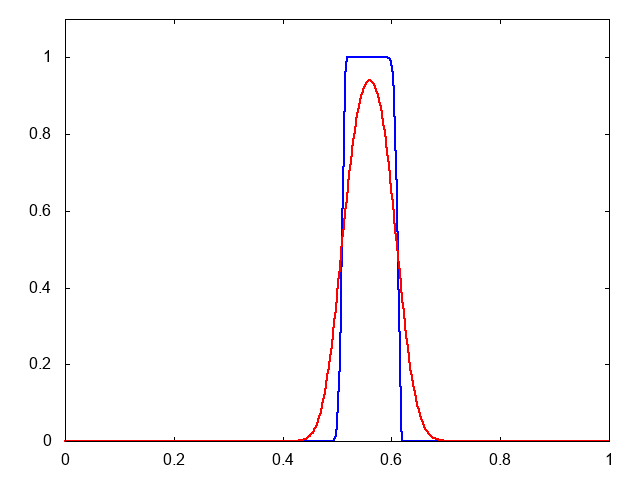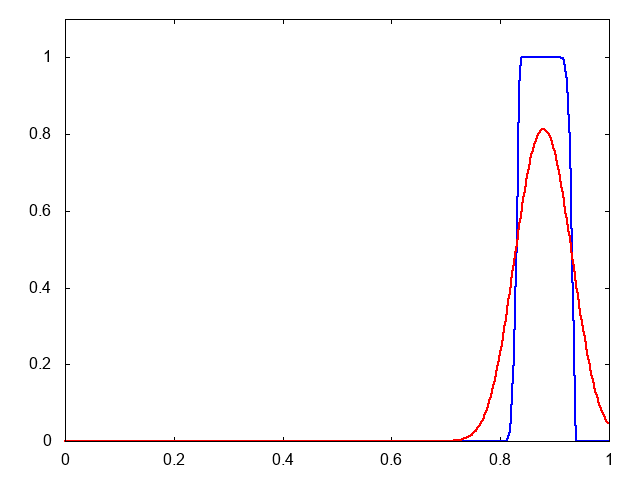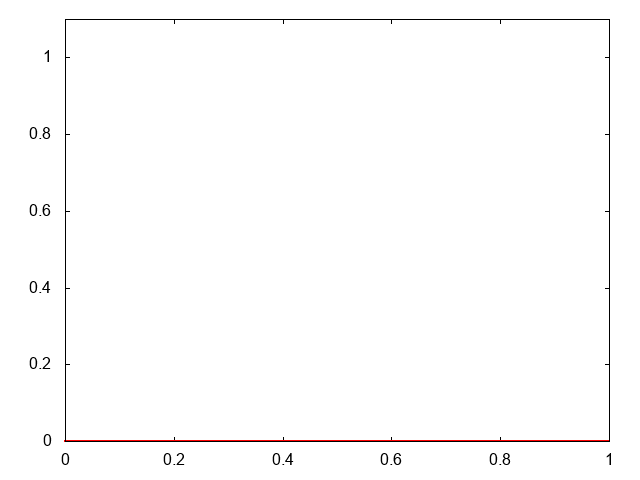
MUSCLのほうが初期プロファイルをよく保っているのがわかります。また、1次の風上差分の数値粘性の大きさもわかります。こんなに拡散されているのですね。


では、計算コードです。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <string>
#include <sstream>

using namespace std;

//flux for advection equation//
inline double Fluxadv(double V, double uL, double uR)
{
	return max(V,0.0)*uL-max(-V,0.0)*uR;
}

//flux limiter minmod//
inline double minmod(double d1, double d2)
{
	if(d1*d2<=0)
	{
		return 0.0;
	}
	else if(abs(d1)<abs(d2))
	{
		return d1;
	}
	else
	{
		return d2;
	}
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double u[], double uiL[], double uiR[])
{
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dul=u[i]-u[i-1];
		double dur=u[i+1]-u[i];
		
		//slope with slope limiter//
		double k=0.0;
		double b=(3.0-k)/(1.0-k);
		double dulLim=minmod(dur,b*dul);
		double durLim=minmod(dul,b*dur);
		
		double delu=(1.0+k)/2.0*dulLim+(1.0-k)/2.0*durLim;
		
		//boundary extrapolation//
		uiL[i]=u[i]-0.5*delu;
		uiR[i]=u[i]+0.5*delu;
	}
	
	//BC//
	//i=0//
	uiL[0]=uiL[1];
	uiR[0]=uiR[1];
	
	//i=Node-1//
	uiL[Node-1]=uiL[Node-2];
	uiR[Node-1]=uiR[Node-2];
}

inline void output(double u[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="u_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<u[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	count+=1;
}

int main()
{
	const int Cell=400;
	const int Node=Cell+1;
	int div=100;//for output
	double LL=1.0;
	double dx=LL/(Node-1);
	double dt=0.001;
	double TotalTime=10;
	double V=0.1;
	double u[Node];
	double ub[Node];
	double un[Node];
	double FL;
	double FR;
	double uiL[Node];
	double uiR[Node];
	
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		u[i]=0.0;
		if((i>=80)&&(i<=120)) u[i]=1.0;
	}
	
	//IC output//
	output(u,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,u,uiL,uiR);
		
		//inner cells//
		for(int i=1;i<Node-1;i++)
		{
			//FR=Fluxadv(V,u[i],u[i+1]);
			//FL=Fluxadv(V,u[i-1],u[i]);
			FR=Fluxadv(V,uiR[i],uiL[i+1]);
			FL=Fluxadv(V,uiR[i-1],uiL[i]);
			un[i]=u[i]-dt/dx*(FR-FL);
		}

		//BC//
		//left boundary//
		un[0]=un[1];

		//right boundary//
		un[Node-1]=un[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			u[i]=un[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(u,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}


こちらではToro流のslope limiterを入れてあります。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <string>
#include <sstream>

using namespace std;

//flux for advection equation//
inline double Fluxadv(double V, double uL, double uR)
{
	return max(V,0.0)*uL-max(-V,0.0)*uR;
}

//flux limiter superbee//
inline double superbee(double d1, double d2, double delta, double omega)
{
	double zeta;

	if(d1*d2<=0)
	{
		zeta=0.0;
	}
	else
	{
		if(d1/d2<=0.5)
		{
			zeta=2.0*d1/d2;
		}
		else if(d1/d2<=1.0)
		{
			zeta=1.0;
		}
		else
		{
			double zetaR=2.0/(1.0-omega+(1.0+omega)*d1/d2);
			zeta=min(zetaR,d1/d2);
			zeta=min(zeta,2.0);
		}
	}
	
	return zeta*delta;
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double u[], double uiL[], double uiR[])
{
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dul=u[i]-u[i-1];
		double dur=u[i+1]-u[i];
		
		//slope//
		double omega=0.0;
		double delu=(1.0+omega)/2.0*dul+(1.0-omega)/2.0*dur;
		
		//slope limiter//
		delu=superbee(dul,dur,delu,omega);
		
		//boundary extrapolation//
		uiL[i]=u[i]-0.5*delu;
		uiR[i]=u[i]+0.5*delu;
	}
	
	//BC//
	//i=0//
	uiL[0]=uiL[1];
	uiR[0]=uiR[1];
	
	//i=Node-1//
	uiL[Node-1]=uiL[Node-2];
	uiR[Node-1]=uiR[Node-2];
}

inline void output(double u[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="u_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<u[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	count+=1;
}

int main()
{
	const int Cell=800;
	const int Node=Cell+1;
	int div=100;//for output
	double LL=1.0;
	double dx=LL/(Node-1);
	double dt=0.001;
	double TotalTime=10;
	double V=0.1;
	double u[Node];
	double ub[Node];
	double un[Node];
	double FL;
	double FR;
	double uiL[Node];
	double uiR[Node];
	
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		u[i]=0.0;
		if((i>=80)&&(i<=160)) u[i]=1.0;
	}
	
	//IC output//
	output(u,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,u,uiL,uiR);
		
		//inner cells//
		for(int i=1;i<Node-1;i++)
		{
			//FR=Fluxadv(V,u[i],u[i+1]);
			//FL=Fluxadv(V,u[i-1],u[i]);
			FR=Fluxadv(V,uiR[i],uiL[i+1]);
			FL=Fluxadv(V,uiR[i-1],uiL[i]);
			un[i]=u[i]-dt/dx*(FR-FL);
		}

		//BC//
		//left boundary//
		un[0]=un[1];

		//right boundary//
		un[Node-1]=un[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			u[i]=un[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(u,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}

【浅水流方程式】MUSCL-Hancock法とHLL法でダム崩壊問題を解いてみました　動画とC++コード付き

双曲型保存則方程式 数値流体力学 数値計算 有限体積法 浅水流方程式

【浅水流方程式】サイトマップ（ここから関連記事が探せます）
http://mathlang.hatenablog.com/entry/2018/12/18/213650


今回は、HLL法にMUSCL-Hancock法を組み合わせて高次精度化したスキームでダム崩壊問題を解きました。

普通のHLL法が時間・空間方向に対して1次精度なのにたいして、MUSCL-Hancock法を組み合わせたHLL法は、時間・空間方向に対して2次精度になります！普通のGodunov法（有限体積法）では各セルでの未知数は定数としますが、MUSCL-Hancock法では、各セルにおいて未知数は線型に変化するとします。こうすることにより、より高精度な数値流束を求めることが可能となります。また、衝撃波近傍での数値振動を回避するために、slope limiter（勾配制限関数）の一種であるsuperbee limiterを採用しています。


解いている方程式は、摩擦、勾配を無視した1次元浅水流方程式（Shallow Water Equations）です。

\displaystyle \begin{eqnarray} &\frac{\partial h}{\partial t} + \frac{\partial q}{\partial x} = 0 \\ &\frac{\partial q}{\partial t} + \frac{\partial}{\partial x} \left( \frac{q^2}{h} + \frac{1}{2}gh^2 \right) = 0 \end{eqnarray}


参考文献としてはToroの"Shock-Capturing Methods for Free-Surface Shallow Flows"のpp.205-210です。

Shock-Capturing Methods for Free-Surface Shallow Flows

Shock-Capturing Methods for Free-Surface Shallow Flows


こちらが計算結果です。青い線が水深です。

f:id:mutsumunemitsutan:20190706150338g:plain:w500

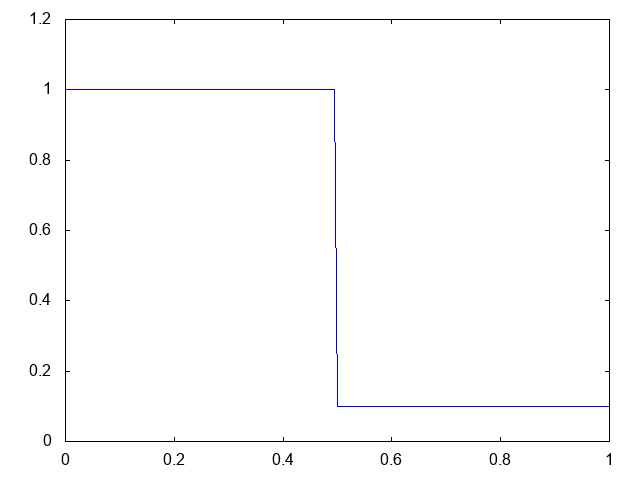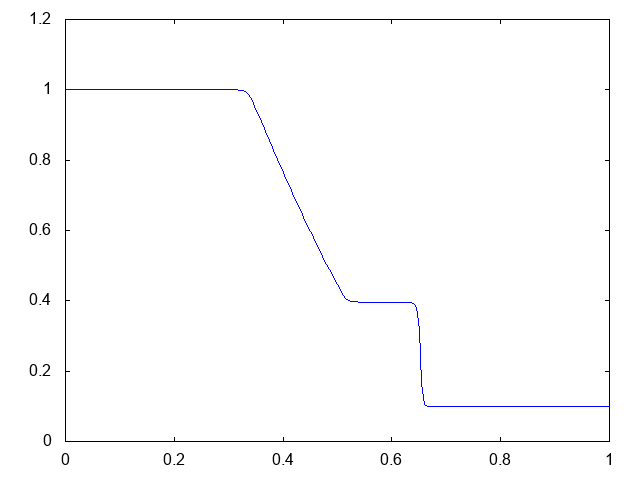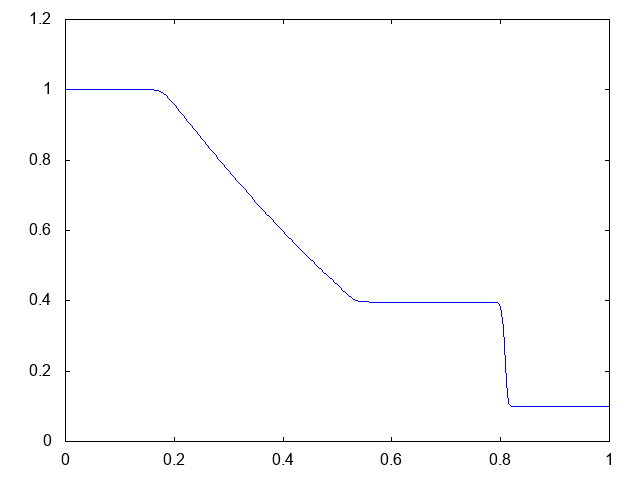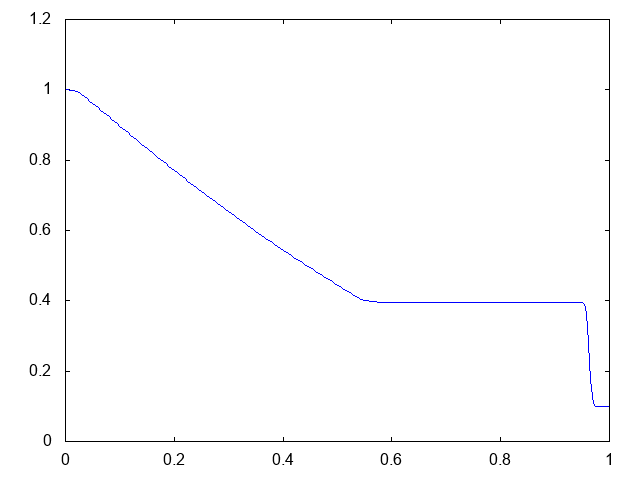
より少ない格子数で、普通のHLL法よりも衝撃波がシャープに捉えられています。


本当にそうだろうか？と疑問を持つ方のために比較動画を用意しました。セル数は100です。青がMUSCL-Hancock法を入れたHLL法で、赤がただのHLL法です。

f:id:mutsumunemitsutan:20190706155659g:plain:w500

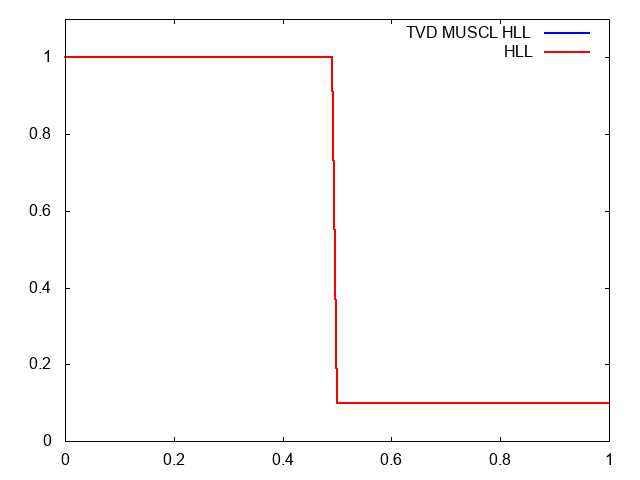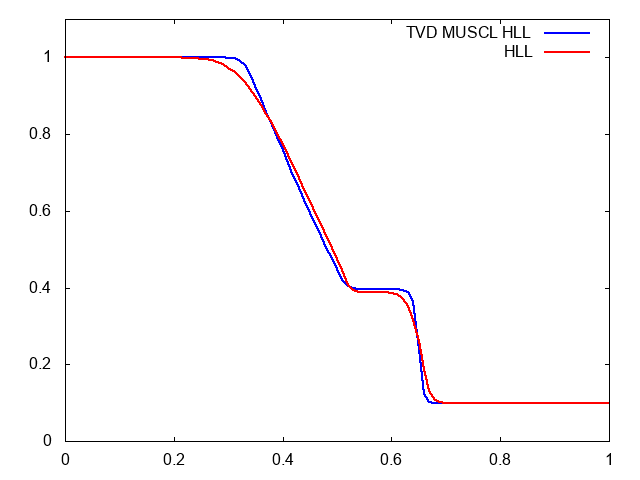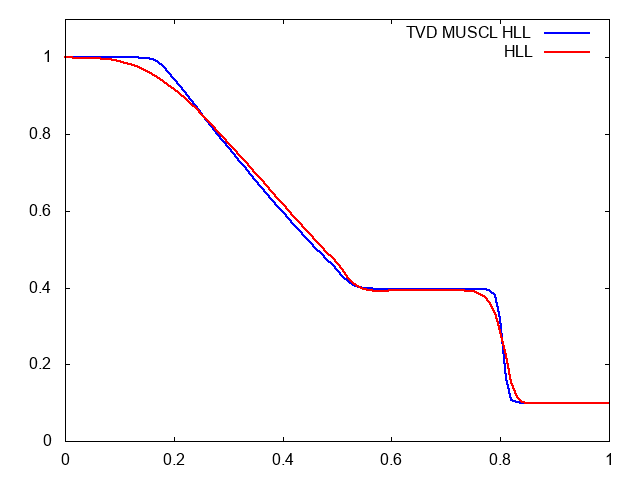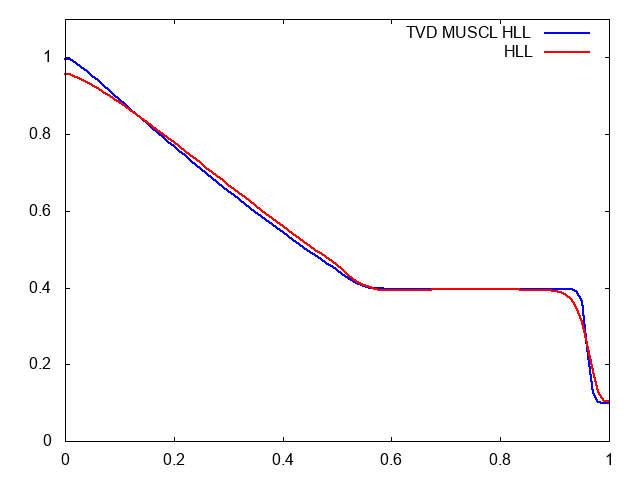
やはりMUSCLのほうが衝撃波の先端がシャープです。しかも、膨張波も角まで捉えられているし、途中の形状もより正確です。


では計算コードです。Toro流のslope limiterが入っています。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <sstream>

using namespace std;

const double g=9.8;

//celerity//
inline double a(double h)
{
	return sqrt(g*h);
}

//function for TRRS//
inline double gk(double h0, double hlr)
{
	return sqrt(g/2.0*(h0+hlr)/(h0*hlr));
}

//Riemann Solver Based on Exact Depth Positivity//
inline void EDPRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=(hL+hR)/2.0-(uR-uL)*(hL+hR)/4.0/(aL+aR);
	ust=(uL+uR)/2.0-(hR-hL)*(aL+aR)/(hL+hR);
}

//Two-Rarefaction Riemann Solver//
inline void TRRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=1.0/g*((aL+aR)/2.0+(uL-uR)/4.0)*((aL+aR)/2.0+(uL-uR)/4.0);
	ust=(uL+uR)/2.0+aL-aR;
}

//Two-Shock Riemann Solver//
inline void TSRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double uL=qL/hL;
	double uR=qR/hR;
	
	TRRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	double hcon=hst;
	hst=(gk(hst,hL)*hL+gk(hst,hR)*hR+uL-uR)/(gk(hst,hL)+gk(hst,hR));
	ust=(uL+uR)/2.0+((hcon-hR)*gk(hcon,hR)-(hcon-hL)*gk(hcon,hL))/2.0;
}

//function for HLL//
inline double qk(double hst, double hlr)
{
	double qk=1.0;
	if(hst>hlr) qk=sqrt((hst+hlr)*hst/(hlr*hlr)/2.0);
	return qk;
}


//left wave estimation//
inline double SLeft(double hst, double hL, double qL)
{
	double uL=qL/hL;
	return uL-a(hL)*qk(hst,hL);
}

//right wave estimation//
inline double SRight(double hst, double hR, double qR)
{
	double uR=qR/hR;
	return uR+a(hR)*qk(hst,hR);
}

//flux for continuity equation//
inline double Fluxcon(double h, double q)
{
	return q;
}

//flux for momentum equation//
inline double Fluxmom(double h, double q)
{
	return q*q/h+g*h*h/2.0;

}

//hll flux//
inline void HLLFlux(double FLR[], double hL, double hR, double qL, double qR)
{
	double hst,ust;

	//estimastion of hst and ust//
	TRRS(hst,ust,hL,hR,qL,qR);
	//TSRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	
	//wave speed estimation//
	double SL=SLeft(hst,hL,qL);
	double SR=SRight(hst,hR,qR);
	
	if(SL>=0)
	{
		FLR[0]=Fluxcon(hL,qL);
		FLR[1]=Fluxmom(hL,qL);
	}
	else if(SR<=0)
	{
		FLR[0]=Fluxcon(hR,qR);
		FLR[1]=Fluxmom(hR,qR);
	}
	else
	{
		FLR[0]=(SR*Fluxcon(hL,qL)-SL*Fluxcon(hR,qR)+SR*SL*(hR-hL))/(SR-SL);
		FLR[1]=(SR*Fluxmom(hL,qL)-SL*Fluxmom(hR,qR)+SR*SL*(qR-qL))/(SR-SL);
	}
}

inline void output(double h[], double z[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="h_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<h[i]+z[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<z[i]<<endl;
	}
	
	count+=1;
}

//flux limiter superbee//
inline double superbee(double d1, double d2, double delta, double omega)
{
	double zeta;

	if(d1*d2<=0)
	{
		zeta=0.0;
	}
	else
	{
		if(d1/d2<=0.5)
		{
			zeta=2.0*d1/d2;
		}
		else if(d1/d2<=1.0)
		{
			zeta=1.0;
		}
		else
		{
			double zetaR=2.0/(1.0-omega+(1.0+omega)*d1/d2);
			zeta=min(zetaR,d1/d2);
			zeta=min(zeta,2.0);
		}
	}
	
	return zeta*delta;
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double h[], double q[], double hiLn[], double hiRn[], double qiLn[], double qiRn[])
{
	double hiL[Node];
	double hiR[Node];
	double qiL[Node];
	double qiR[Node];
	
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dhl=h[i]-h[i-1];
		double dhr=h[i+1]-h[i];
		double dql=q[i]-q[i-1];
		double dqr=q[i+1]-q[i];
		
		//slope//
		double omega=0.0;
		double delh=(1.0+omega)/2.0*dhl+(1.0-omega)/2.0*dhr;
		double delq=(1.0+omega)/2.0*dql+(1.0-omega)/2.0*dqr;
		
		//slope limiter//
		delh=superbee(dhl,dhr,delh,omega);
		delq=superbee(dql,dqr,delq,omega);
		
		//boundary extrapolation//
		hiL[i]=h[i]-0.5*delh;
		hiR[i]=h[i]+0.5*delh;
		qiL[i]=q[i]-0.5*delq;
		qiR[i]=q[i]+0.5*delq;
	
		//time evolution of boundary extrapolated values//
		hiLn[i]=hiL[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		hiRn[i]=hiR[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		qiLn[i]=qiL[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
		qiRn[i]=qiR[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
	}
	
	//BC//
	//i=0//
	hiLn[0]=hiLn[1];
	hiRn[0]=hiRn[1];
	qiLn[0]=qiLn[1];
	qiRn[0]=qiRn[1];
	
	//i=Node-1//
	hiLn[Node-1]=hiLn[Node-2];
	hiRn[Node-1]=hiRn[Node-2];
	qiLn[Node-1]=qiLn[Node-2];
	qiRn[Node-1]=qiRn[Node-2];
}

int main()
{
	const int n=200;//number of cells
	const int Node=n+1;
	double L=1.0;
	double dx=L/double(n);
	double dt=0.0001;
	double TotalTime=0.15;
	int div=20;//for output
	double q[Node];
	double h[Node];
	double qn[Node];
	double hn[Node];
	double FL[2],FR[2];
	double InithL=1.0;
	double InithR=0.1;
	double z[Node];
	double I[Node];
	double mn=0.01;
	//for reconstruction//
	double hiLn[Node];
	double hiRn[Node];
	double qiLn[Node];
	double qiRn[Node];
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithL;
	}
	for(int i=Node/2;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithR;
	}
	
	//bottom//
	for(int i=0;i<Node;i++)
	{
		z[i]=0.0;
		double a=0.1-3.0*(float(i)*dx-0.5)*(float(i)*dx-0.5);
		if(a>0.0) z[i]=a;
		z[i]=0.0;
		//cout<<z[i]<<endl;
	}
	
	//slope//
	for(int i=1;i<Node-1;i++)
	{
		I[i]=-(z[i]-z[i-1])/dx;
	}
	//at boundary// 
	I[0]=-(z[1]-z[0])/dx;
	I[Node-1]=-(z[Node-1]-z[Node-2])/dx;
	
	//IC output//
	output(h,z,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,h,q,hiLn,hiRn,qiLn,qiRn);
		
		//HLL//
		for(int i=1;i<Node-1;i++)
		{
			//left flux, between i-1 and i//i-1R,iL
			HLLFlux(FL,hiRn[i-1],hiLn[i],qiRn[i-1],qiLn[i]);
			
			//right flux, between i and i+1//iR,i+1L
			HLLFlux(FR,hiRn[i],hiLn[i+1],qiRn[i],qiLn[i+1]);
			
			hn[i]=h[i]-dt/dx*(FR[0]-FL[0]);
			qn[i]=q[i]-dt/dx*(FR[1]-FL[1]);//+dt*g*h[i]*(I[i]-mn*mn*q[i]*abs(q[i])/pow(h[i],10.0/3.0));
		}

		//BC//
		//left boundary//
		hn[0]=hn[1];
		qn[0]=qn[1];

		//right boundary//
		hn[Node-1]=hn[Node-2];
		qn[Node-1]=qn[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			q[i]=qn[i];
			h[i]=hn[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(h,z,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}


こちらは一般的なMUSCLに書き直したほうです。両者はほぼ一致します。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <sstream>

using namespace std;

const double g=9.8;

//celerity//
inline double a(double h)
{
	return sqrt(g*h);
}

//function for TRRS//
inline double gk(double h0, double hlr)
{
	return sqrt(g/2.0*(h0+hlr)/(h0*hlr));
}

//Riemann Solver Based on Exact Depth Positivity//
inline void EDPRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=(hL+hR)/2.0-(uR-uL)*(hL+hR)/4.0/(aL+aR);
	ust=(uL+uR)/2.0-(hR-hL)*(aL+aR)/(hL+hR);
}

//Two-Rarefaction Riemann Solver//
inline void TRRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=1.0/g*((aL+aR)/2.0+(uL-uR)/4.0)*((aL+aR)/2.0+(uL-uR)/4.0);
	ust=(uL+uR)/2.0+aL-aR;
}

//Two-Shock Riemann Solver//
inline void TSRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double uL=qL/hL;
	double uR=qR/hR;
	
	TRRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	double hcon=hst;
	hst=(gk(hst,hL)*hL+gk(hst,hR)*hR+uL-uR)/(gk(hst,hL)+gk(hst,hR));
	ust=(uL+uR)/2.0+((hcon-hR)*gk(hcon,hR)-(hcon-hL)*gk(hcon,hL))/2.0;
}

//function for HLL//
inline double qk(double hst, double hlr)
{
	double qk=1.0;
	if(hst>hlr) qk=sqrt((hst+hlr)*hst/(hlr*hlr)/2.0);
	return qk;
}


//left wave estimation//
inline double SLeft(double hst, double hL, double qL)
{
	double uL=qL/hL;
	return uL-a(hL)*qk(hst,hL);
}

//right wave estimation//
inline double SRight(double hst, double hR, double qR)
{
	double uR=qR/hR;
	return uR+a(hR)*qk(hst,hR);
}

//flux for continuity equation//
inline double Fluxcon(double h, double q)
{
	return q;
}

//flux for momentum equation//
inline double Fluxmom(double h, double q)
{
	return q*q/h+g*h*h/2.0;

}

//hll flux//
inline void HLLFlux(double FLR[], double hL, double hR, double qL, double qR)
{
	double hst,ust;

	//estimastion of hst and ust//
	TRRS(hst,ust,hL,hR,qL,qR);
	//TSRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	
	//wave speed estimation//
	double SL=SLeft(hst,hL,qL);
	double SR=SRight(hst,hR,qR);
	
	if(SL>=0)
	{
		FLR[0]=Fluxcon(hL,qL);
		FLR[1]=Fluxmom(hL,qL);
	}
	else if(SR<=0)
	{
		FLR[0]=Fluxcon(hR,qR);
		FLR[1]=Fluxmom(hR,qR);
	}
	else
	{
		FLR[0]=(SR*Fluxcon(hL,qL)-SL*Fluxcon(hR,qR)+SR*SL*(hR-hL))/(SR-SL);
		FLR[1]=(SR*Fluxmom(hL,qL)-SL*Fluxmom(hR,qR)+SR*SL*(qR-qL))/(SR-SL);
	}
}

inline void output(double h[], double z[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="h_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<h[i]+z[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<z[i]<<endl;
	}
	
	count+=1;
}

//flux limiter minmod//
inline double minmod(double d1, double d2)
{
	if(d1*d2<=0)
	{
		return 0.0;
	}
	else if(abs(d1)<abs(d2))
	{
		return d1;
	}
	else
	{
		return d2;
	}
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double h[], double q[], double hiLn[], double hiRn[], double qiLn[], double qiRn[])
{
	double hiL[Node];
	double hiR[Node];
	double qiL[Node];
	double qiR[Node];
	
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dhl=h[i]-h[i-1];
		double dhr=h[i+1]-h[i];
		double dql=q[i]-q[i-1];
		double dqr=q[i+1]-q[i];
		
		
		
		//slope limiter//
		double k=0.0;
		double b=(3.0-k)/(1.0-k);
		double dhlLim=minmod(dhr,b*dhl);
		double dhrLim=minmod(dhl,b*dhr);
		double dqlLim=minmod(dqr,b*dql);
		double dqrLim=minmod(dql,b*dqr);
		
		double omega=0.0;
		double delh=(1.0+omega)/2.0*dhlLim+(1.0-omega)/2.0*dhrLim;
		double delq=(1.0+omega)/2.0*dqlLim+(1.0-omega)/2.0*dqrLim;
		
		
		//boundary extrapolation//
		hiL[i]=h[i]-0.5*delh;
		hiR[i]=h[i]+0.5*delh;
		qiL[i]=q[i]-0.5*delq;
		qiR[i]=q[i]+0.5*delq;
	
		//time evolution of boundary extrapolated values//
		hiLn[i]=hiL[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		hiRn[i]=hiR[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		qiLn[i]=qiL[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
		qiRn[i]=qiR[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
	}
	
	//BC//
	//i=0//
	hiLn[0]=hiLn[1];
	hiRn[0]=hiRn[1];
	qiLn[0]=qiLn[1];
	qiRn[0]=qiRn[1];
	
	//i=Node-1//
	hiLn[Node-1]=hiLn[Node-2];
	hiRn[Node-1]=hiRn[Node-2];
	qiLn[Node-1]=qiLn[Node-2];
	qiRn[Node-1]=qiRn[Node-2];
}

int main()
{
	const int n=200;//number of cells
	const int Node=n+1;
	double L=1.0;
	double dx=L/double(n);
	double dt=0.0001;
	double TotalTime=0.15;
	int div=20;//for output
	double q[Node];
	double h[Node];
	double qn[Node];
	double hn[Node];
	double FL[2],FR[2];
	double InithL=1.0;
	double InithR=0.1;
	double z[Node];
	double I[Node];
	double mn=0.01;
	//for reconstruction//
	double hiLn[Node];
	double hiRn[Node];
	double qiLn[Node];
	double qiRn[Node];
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithL;
	}
	for(int i=Node/2;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithR;
	}
	
	//bottom//
	for(int i=0;i<Node;i++)
	{
		z[i]=0.0;
		double a=0.1-3.0*(float(i)*dx-0.5)*(float(i)*dx-0.5);
		if(a>0.0) z[i]=a;
		z[i]=0.0;
		//cout<<z[i]<<endl;
	}
	
	//slope//
	for(int i=1;i<Node-1;i++)
	{
		I[i]=-(z[i]-z[i-1])/dx;
	}
	//at boundary// 
	I[0]=-(z[1]-z[0])/dx;
	I[Node-1]=-(z[Node-1]-z[Node-2])/dx;
	
	//IC output//
	output(h,z,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,h,q,hiLn,hiRn,qiLn,qiRn);
		
		//HLL//
		for(int i=1;i<Node-1;i++)
		{
			//left flux, between i-1 and i//i-1R,iL
			HLLFlux(FL,hiRn[i-1],hiLn[i],qiRn[i-1],qiLn[i]);
			
			//right flux, between i and i+1//iR,i+1L
			HLLFlux(FR,hiRn[i],hiLn[i+1],qiRn[i],qiLn[i+1]);
			
			hn[i]=h[i]-dt/dx*(FR[0]-FL[0]);
			qn[i]=q[i]-dt/dx*(FR[1]-FL[1]);//+dt*g*h[i]*(I[i]-mn*mn*q[i]*abs(q[i])/pow(h[i],10.0/3.0));
		}

		//BC//
		//left boundary//
		hn[0]=hn[1];
		qn[0]=qn[1];

		//right boundary//
		hn[Node-1]=hn[Node-2];
		qn[Node-1]=qn[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			q[i]=qn[i];
			h[i]=hn[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(h,z,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}

【浅水流方程式】HLLC法でダム崩壊問題を解いてみました（wet bedとdry bed）　動画とC++コード付き

双曲型保存則方程式 数値流体力学 数値計算 有限体積法 浅水流方程式

【浅水流方程式】サイトマップ（ここから関連記事が探せます）
http://mathlang.hatenablog.com/entry/2018/12/18/213650


今回は、HLLC法（Harten, Lax, van Leer, Contact surface法）を用いてダム崩壊問題（dam break problem）を解いてみました。HLLC法とは、HLL法を発展させたもので、波速が最大のものと最小のものに加えて、contact discontinuity（接触不連続、shear wave）を考慮し、全体を4つの状態に分けて解く手法です。Toro教授が考案しました。2×2の普通の1次元浅水流方程式を解く上では、contact discontinuityはあらわれないのですが、1次元浅水流方程式と溶質の濃度を考える場合、1次元浅水流方程式と移動床を考える場合、2次元浅水流方程式などの3×3のシステムを解く際には、contact discontinuityがあらわれます。HLLC法を用いると、このcontact discontinuityを捉えることができるようになります。解いている方程式は、摩擦、勾配なしの1次元浅水流方程式（Shallow Water Equations）に溶質の濃度を考慮した3×3の以下のシステムです。

\displaystyle \begin{eqnarray} &\frac{\partial h}{\partial t} + \frac{\partial q}{\partial x} = 0 \\ &\frac{\partial q}{\partial t} + \frac{\partial}{\partial x} \left( \frac{q^2}{h} + \frac{1}{2}gh^2 \right) = 0 \\ &\frac{\partial (h \phi) }{\partial t} + \frac{\partial (uh \phi)}{\partial x} = 0 \end{eqnarray}

ここで \phi はpassiveな溶質の濃度です。参考文献はLeVequeの"Finite Volume Methods for Hyperbolic Problems"のpp.283-285です。

Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics)

Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics)

初期状態としては、wet bedの場合は、領域のちょうど左側で水深が1.0、領域のちょうど右側で水深が0.1で、水面は静止しているものとします。また、濃度に関しては、左側で1.0、右側で0とします。dry bedの場合は、領域のちょうど左側で水深が1.0、領域のちょうど右側で水深が 10^{-7} で、水面は静止しているものとします。このように、dry bedの場合は非常に小さい水深を与えることとします。濃度に関しては同じです。時刻 t=0 に真ん中にあるしきり（ダム）を取り去った時に、水がどのように動くかを計算します。境界条件としては右端、左端で水深、流量、濃度ともに斉次のノイマン条件を課しています。


参考文献としてはToroの"Shock-Capturing Methods for Free-Surface Shallow Flows"のpp.181-183です。バイブルですね。波速を推定するための手法としては、Exact Depth Positivity Riemann Solver (EDPRS)、Two-Rarefaction Riemann Solver (TRRS)、Two-Shock Riemann Solver (TSRS) を選べるようになっています。

Shock-Capturing Methods for Free-Surface Shallow Flows

Shock-Capturing Methods for Free-Surface Shallow Flows


こちらがwet bedの場合の水深の計算結果です。水深が青い線で表示されています。

f:id:mutsumunemitsutan:20190630231223g:plain:w500

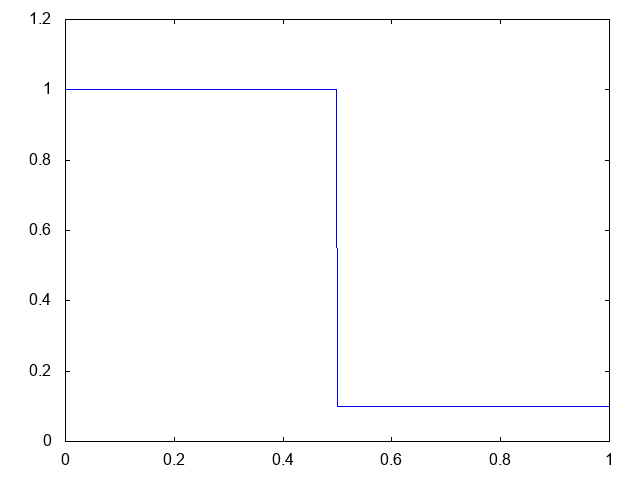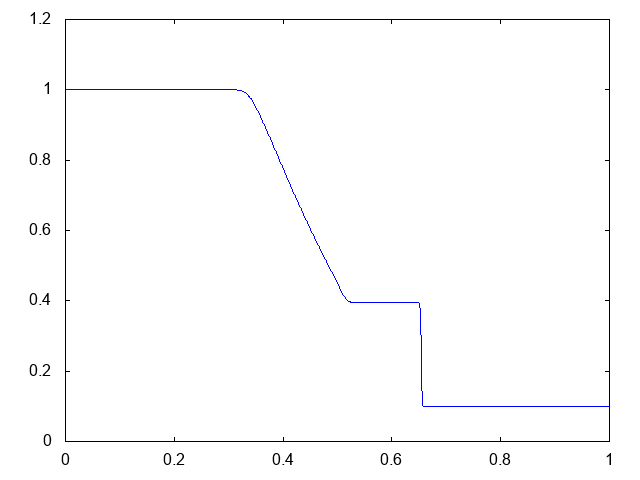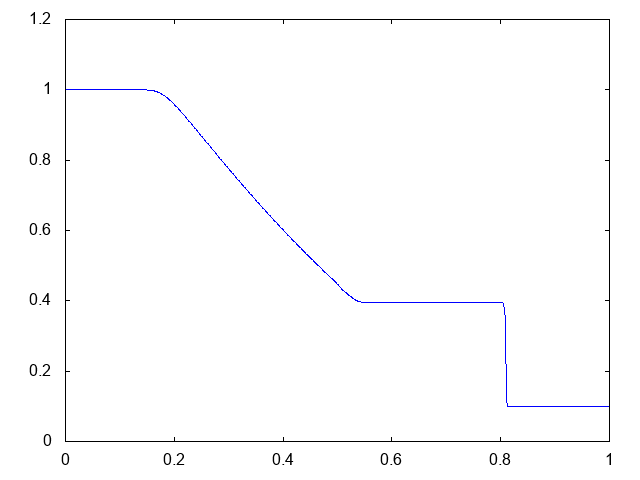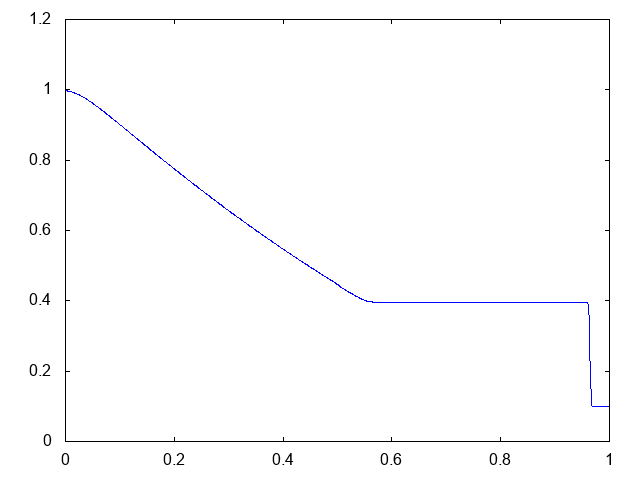
右へと進行する衝撃波（不連続な波、Shock wave）と左へと進行する膨張波（連続な波、Rarefaction wave）が観察できます。よい感じです。これはHLLとほぼ同じ結果です。

こちらがwet bedの場合の溶質濃度の計算結果です。青い線で溶質の濃度が表示されています。

f:id:mutsumunemitsutan:20190706152517g:plain:w500

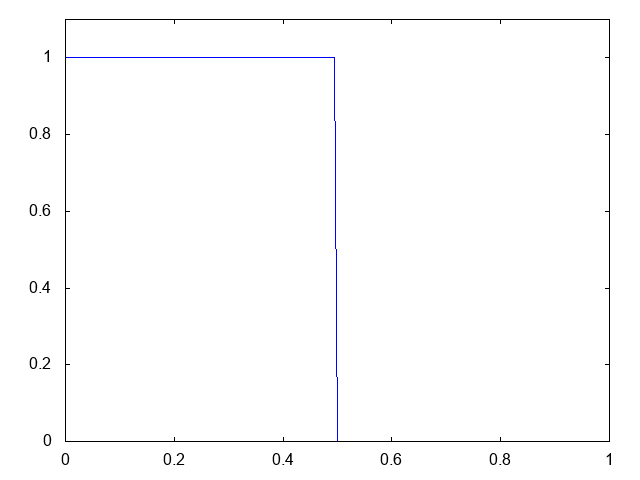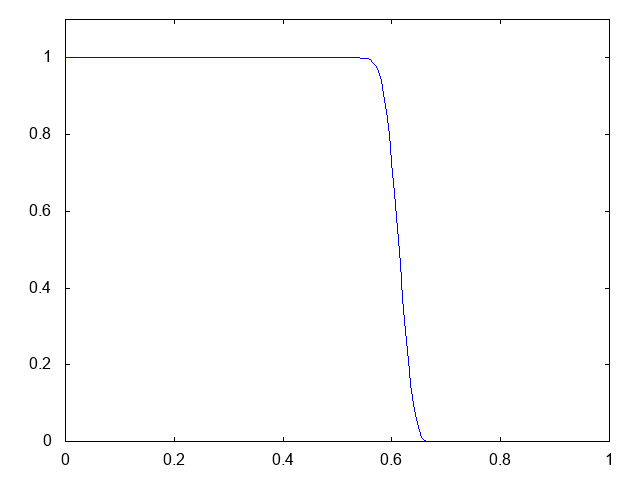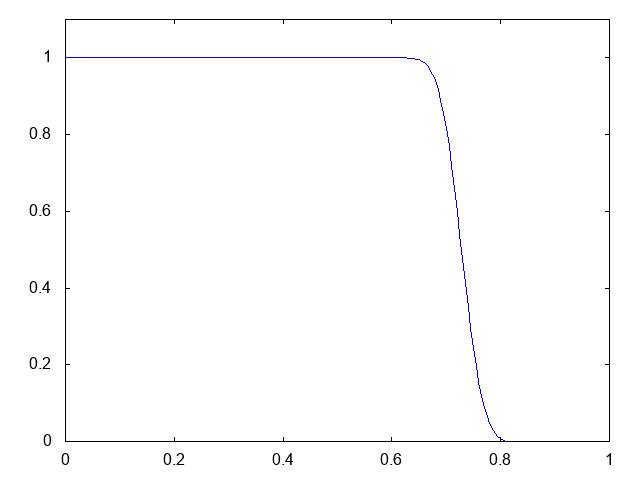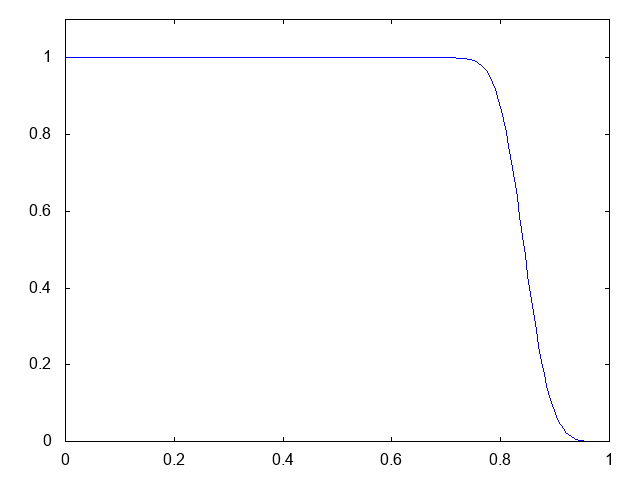
初期時刻にステップ上に分布していた溶質の濃度が、ダムが崩壊すると同時に右方向へと流れていきます。厳密解はステップの形状を保つものです。


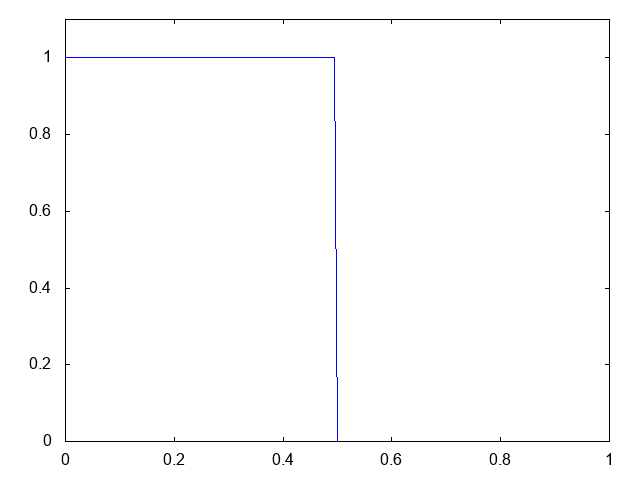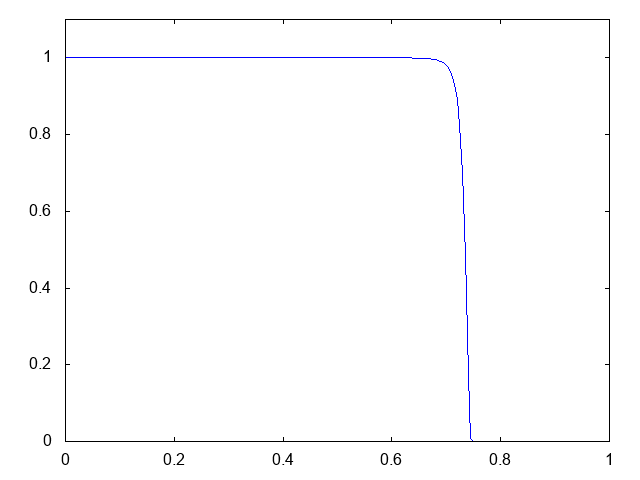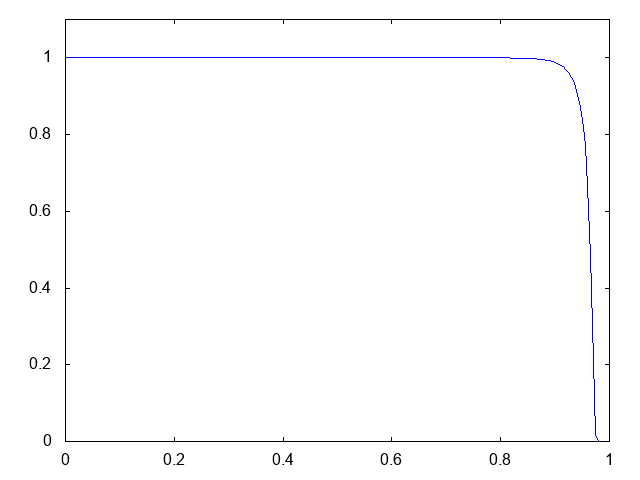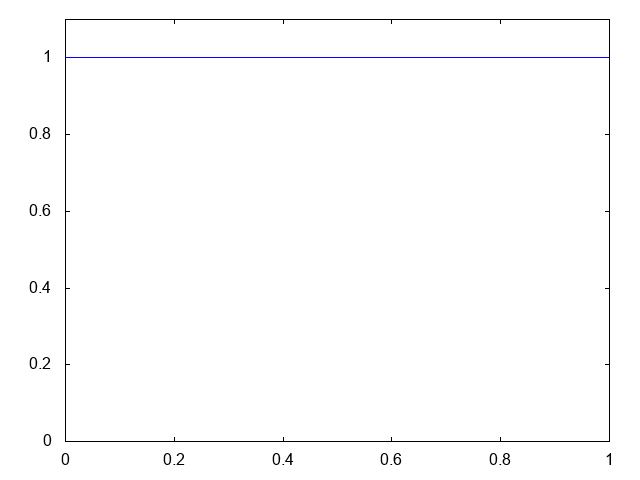
こちらがdry bedの場合の水深の計算結果です。

f:id:mutsumunemitsutan:20190706153010g:plain:w500

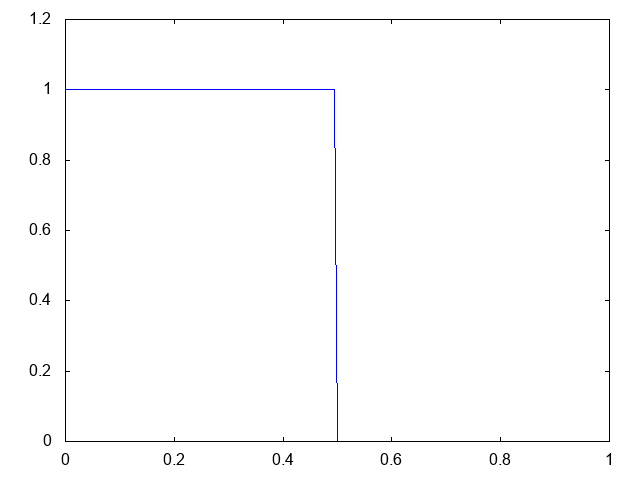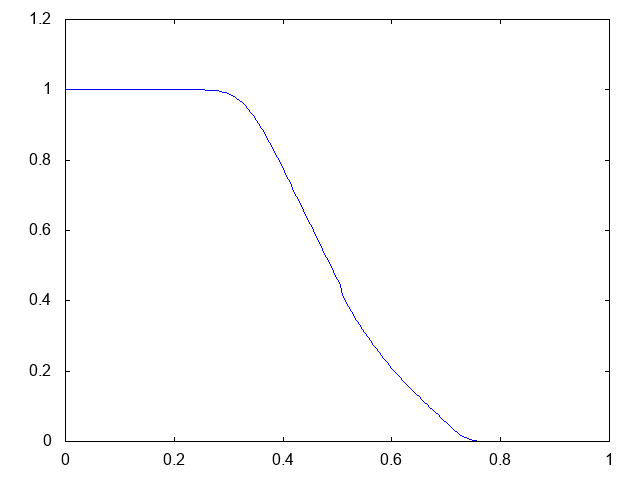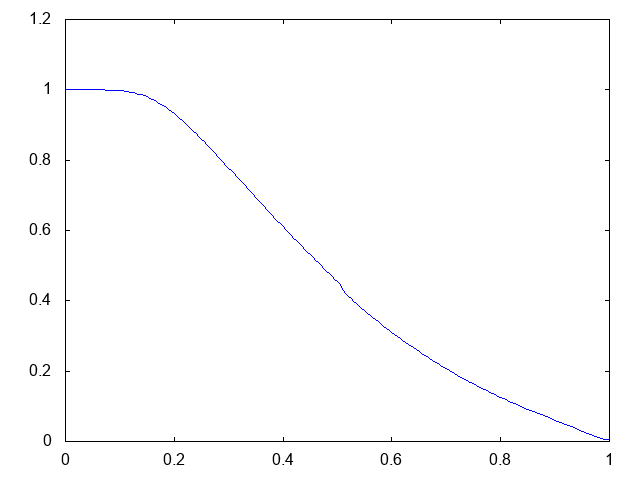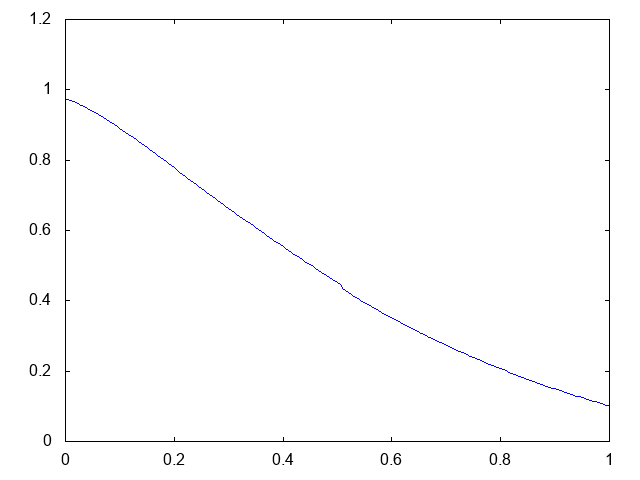
右へと進行する膨張波（連続な波、Rarefaction wave）が観察できます。よい感じです。

こちらがdry bedの場合の溶質濃度の計算結果です。

f:id:mutsumunemitsutan:20190706152905g:plain:w500

初期時刻にステップ上に分布していた溶質の濃度が、ダムが崩壊すると同時に右方向へと流れていきます。厳密解はステップの形状を保つものです。


では計算コードです。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <sstream>

using namespace std;

const double g=9.8;

//celerity//
inline double a(double h)
{
	return sqrt(g*h);
}

//function for TRRS//
inline double gk(double h0, double hlr)
{
	return sqrt(g/2.0*(h0+hlr)/(h0*hlr));
}

//Riemann Solver Based on Exact Depth Positivity//
inline void EDPRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=(hL+hR)/2.0-(uR-uL)*(hL+hR)/4.0/(aL+aR);
	ust=(uL+uR)/2.0-(hR-hL)*(aL+aR)/(hL+hR);
}

//Two-Rarefaction Riemann Solver//
inline void TRRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=1.0/g*((aL+aR)/2.0+(uL-uR)/4.0)*((aL+aR)/2.0+(uL-uR)/4.0);
	ust=(uL+uR)/2.0+aL-aR;
}

//Two-Shock Riemann Solver//
inline void TSRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double uL=qL/hL;
	double uR=qR/hR;
	
	TRRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	double hcon=hst;
	hst=(gk(hst,hL)*hL+gk(hst,hR)*hR+uL-uR)/(gk(hst,hL)+gk(hst,hR));
	ust=(uL+uR)/2.0+((hcon-hR)*gk(hcon,hR)-(hcon-hL)*gk(hcon,hL))/2.0;
}

//function for HLL//
inline double qk(double hst, double hlr)
{
	double qk=1.0;
	if(hst>hlr) qk=sqrt((hst+hlr)*hst/(hlr*hlr)/2.0);
	return qk;
}


//left wave estimation//
inline double SLeft(double hst, double hL, double qL)
{
	double uL=qL/hL;
	return uL-a(hL)*qk(hst,hL);
}

//right wave estimation//
inline double SRight(double hst, double hR, double qR)
{
	double uR=qR/hR;
	return uR+a(hR)*qk(hst,hR);
}

//shear wave estimation//
inline double SShear(double hst, double ust, double hL, double hR, double qL, double qR, double SL, double SR)
{
	double uR=qR/hR;
	double uL=qL/hL;
	return (SL*hR*(uR-SR)-SR*hL*(uL-SL))/(hR*(uR-SR)-hL*(uL-SL));
}

//flux for continuity equation//
inline double Fluxcon(double h, double q)
{
	return q;
}

//flux for momentum equation//
inline double Fluxmom(double h, double q)
{
	return q*q/h+g*h*h/2.0;

}

//flux for shear wave//
inline double Fluxshear(double h, double q, double p)
{
	return p*q/h;
}

//hllc flux//
inline void HLLCFlux(double FLR[], double hL, double hR, double qL, double qR, double pL, double pR)
{
	double hst,ust;
	double uR=qR/hR;
	double uL=qL/hL;

	//estimastion of hst and ust//
	TRRS(hst,ust,hL,hR,qL,qR);
	//TSRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	
	//wave speed estimation//
	double SL=SLeft(hst,hL,qL);
	double SR=SRight(hst,hR,qR);
	
	//estimation of shear wave//
	double Sst=SShear(hst,ust,hL,hR,qL,qR,SL,SR);
	//double Sst=ust;
	
	if(SL>=0)
	{
		FLR[0]=Fluxcon(hL,qL);
		FLR[1]=Fluxmom(hL,qL);
		FLR[2]=Fluxshear(hL,qL,pL);
	}
	else if((SL<=0)&&(0<=Sst))
	{
		double UstL[3];
		UstL[0]=hL*(SL-uL)/(SL-Sst)*1.0;
		UstL[1]=hL*(SL-uL)/(SL-Sst)*Sst;
		UstL[2]=hL*(SL-uL)/(SL-Sst)*pL/hL;
		
		FLR[0]=Fluxcon(hL,qL)+SL*(UstL[0]-hL);
		FLR[1]=Fluxmom(hL,qL)+SL*(UstL[1]-qL);
		FLR[2]=Fluxshear(hL,qL,pL)+SL*(UstL[2]-pL);
	}
	else if((Sst<=0)&&(0<=SR))
	{
		double UstR[3];
		UstR[0]=hR*(SR-uR)/(SR-Sst)*1.0;
		UstR[1]=hR*(SR-uR)/(SR-Sst)*Sst;
		UstR[2]=hR*(SR-uR)/(SR-Sst)*pR/hR;
		
		FLR[0]=Fluxcon(hR,qR)+SR*(UstR[0]-hR);
		FLR[1]=Fluxmom(hR,qR)+SR*(UstR[1]-qR);
		FLR[2]=Fluxshear(hR,qR,pR)+SR*(UstR[2]-pR);
	}
	else
	{
		FLR[0]=Fluxcon(hR,qR);
		FLR[1]=Fluxmom(hR,qR);
		FLR[2]=Fluxshear(hR,qR,pR);
	}
}

inline void output(double h[], double z[], double p[], int Node, double dx)
{
	stringstream ss;
	string name,name1;
	ofstream fo,ff;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name1=ss.str();
	name="h_" + name + ".txt";
	fo.open(name.c_str ());
	name1="p_" + name1 + ".txt";
	ff.open(name1.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<h[i]+z[i]<<endl;
		ff<<dx*float(i)<<" "<<p[i]/h[i]<<endl;
	}
	fo<<endl;fo<<endl;
	ff<<endl;ff<<endl;
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<z[i]<<endl;
	}
	
	count+=1;
}

int main()
{
	const int n=1000;//number of cells
	const int Node=n+1;
	double L=1.0;
	double dx=L/double(n);
	double dt=0.0001;
	double TotalTime=0.2;
	int div=20;//for output
	double q[Node];
	double h[Node];
	double p[Node];//solutants
	double qn[Node];
	double hn[Node];
	double pn[Node];
	double FL[3],FR[3];
	double InithL=1.0;
	double InithR=0.1;
	double z[Node];
	double I[Node];
	double mn=0.01;
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithL;
		p[i]=InithL;
	}
	for(int i=Node/2;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithR;
		p[i]=0.0;
	}
	
	//bottom//
	for(int i=0;i<Node;i++)
	{
		z[i]=0.0;
		double a=0.1-3.0*(float(i)*dx-0.5)*(float(i)*dx-0.5);
		if(a>0.0) z[i]=a;
		z[i]=0.0;
	}
	
	//slope//
	for(int i=1;i<Node-1;i++)
	{
		I[i]=-(z[i]-z[i-1])/dx;
	}
	//at boundary// 
	I[0]=-(z[1]-z[0])/dx;
	I[Node-1]=-(z[Node-1]-z[Node-2])/dx;
	
	//IC output//
	output(h,z,p,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//inner cells//
		for(int i=1;i<Node-1;i++)
		{
			//left flux, between i-1 and i//
			HLLCFlux(FL,h[i-1],h[i],q[i-1],q[i],p[i-1],p[i]);
			
			//right flux, between i and i+1//
			HLLCFlux(FR,h[i],h[i+1],q[i],q[i+1],p[i],p[i+1]);
			
			hn[i]=h[i]-dt/dx*(FR[0]-FL[0]);
			qn[i]=q[i]-dt/dx*(FR[1]-FL[1]);//+dt*g*h[i]*(I[i]-mn*mn*q[i]*abs(q[i])/pow(h[i],10.0/3.0));
			pn[i]=p[i]-dt/dx*(FR[2]-FL[2]);
		}

		//BC//
		//left boundary//
		hn[0]=hn[1];
		qn[0]=qn[1];
		pn[0]=pn[1];
		
		//right boundary//
		hn[Node-1]=hn[Node-2];
		qn[Node-1]=qn[Node-2];
		pn[Node-1]=pn[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			q[i]=qn[i];
			h[i]=hn[i];
			p[i]=pn[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(h,z,p,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}

【量子力学】『高校数学でわかるシュレディンガー方程式』

量子力学

量子力学の勉強をはじめました！！！実は、中学校の頃から勉強しようと思っていたのですが、気がついたらこんな年になっていました。私が量子力学に興味を持つきっかけとなったのは、テレビアニメ『ゼーガペイン』です。

ゼーガペインはSFアニメというジャンルの作品で、量子力学が大活躍します。量子力学にもとづいて作られた量子兵器、「ゼーガペイン」に乗り、宿敵ナーガ率いる「ガルズオルム」と人類の生存を懸けて戦うのです。また、ネタバレになってしまいますが、人類は既にナーガが作り出した「オルムウイルス」により滅び、量子コンピュータの中にのみ生きるデータとなっています。しかも、そのデータはサーバーの容量の問題から、半年ごとに「リセット」されてしまいます。つまり、4月4日から8月31日までが無限に繰り返されるのです。こうした状況下で、登場人物の心の機微が丁寧に描写されていきます。あとEDが神がかっている。何万回聞いたかわかりません。

ゼーガペインを見て、がつんとやられた私は理系の学問にのめりこんでいきます。しかし、何故量子力学を専攻にしようと思わなかったのは謎ですね。まあ、今から勉強するのでOKです！


というわけで、竹内淳 著『高校数学でわかるシュレディンガー方程式』を読みました。総ページ数は202で4時間ほどで読めました。

高校数学でわかるシュレディンガー方程式―量子力学を学びたい人、ほんとうに理解したい人へ (ブルーバックス)

高校数学でわかるシュレディンガー方程式―量子力学を学びたい人、ほんとうに理解したい人へ (ブルーバックス)

シュレディンガー方程式を最初に導出し、それを解くことによって波動関数がどのように振舞うか調べていきます。回折格子、ド・ブロイ波、光電効果、原子モデル、スピン、核分裂、量子コンピュータなどなど一度は聞いたことがあるけれど互いの関係がよくわかっていない話がスムーズに整理されています。もし数式が苦手な方でもかなり楽しめ、ためになる本でした。


それに加えて、ヨビノリの量子力学の講座全10回を視聴しました。


ヨビノリの動画は本当に素晴らしい。高度な内容でも工夫次第ではなるべくわかりやすく解説できる、ということを教えてくれます。私も見習いたいです。この動画では、トンネル効果の回が非常にエキサイティングでした。もっとヒルベルト空間を勉強して、量子力学を理解していきたいですね。そして、量子コンピュータを目指していきます。

【浅水流方程式】溶質の濃度を考えた場合の浅水流方程式

双曲型保存則方程式 数値流体力学 数値計算 有限体積法 浅水流方程式

【浅水流方程式】サイトマップ（ここから関連記事が探せます）
http://mathlang.hatenablog.com/entry/2018/12/18/213650

溶質の濃度を考えた場合の浅水流方程式は以下のようになります。

\displaystyle \begin{eqnarray} &\frac{\partial h}{\partial t} + \frac{\partial q}{\partial x} = 0 \\ &\frac{\partial q}{\partial t} + \frac{\partial}{\partial x} \left( \frac{q^2}{h} + \frac{1}{2}gh^2 \right) = 0 \\ &\frac{\partial (h \phi) }{\partial t} + \frac{\partial (uh \phi)}{\partial x} = 0 \end{eqnarray}

ここで \phi はpassiveな溶質の濃度です。参考文献はLeVequeの"Finite Volume Methods for Hyperbolic Problems"のpp.283-285です。

Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics)

Finite Volume Methods for Hyperbolic Problems (Cambridge Texts in Applied Mathematics)

【確率過程】第2章「確率論の概要」の 2.1「確率測度と確率空間」

数学 最適制御 確率論 確率過程 解析学

はじめに

兼清泰明 著『確率微分方程式とその応用』を読んでいきます。今回は第2章「確率論の概要」の 2.1「確率測度と確率空間」を読みます。なるべく定理や命題、式の意味を書いていきたいですね。

確率微分方程式とその応用

確率微分方程式とその応用

第2章「確率論の概要」

  • 準備として確率論の基本事項の概要を述べる
  • 現代確率論には測度論が必須

2.1 確率測度と確率空間

大事なのは、標本空間における全ての部分集合を事象として取り扱わない、ということではないでしょうか。つまり、事象（取り扱う対象）はある満たすべき性質を持つものだけに限る、ということです。これが定義 2.1.1です。つまり、

  • 全体は事象である
  • A が事象であるとき A^c も事象である
  • 可算無限個の事象があるとき、その和集合も事象である

という性質です。最後の性質は完全加法性と呼ばれている重要なものです。この3条件を満たす集合族を \sigma 加法族（完全加法族、 \sigma-field、 \sigma-algebra）と呼び、その要素を事象とします。集合演算を可算無限回まで許容している点が重要です。

次に、確率を定義します。確率とは、事象に値を割り当てる関数（写像）のことです。確率にも満たすべき性質があります。それが定義 2.1.2です。つまり、

  • 確率は0以上である
  • 全事象に対する確率は1である
  • 可算無限個の事象があり、それぞれに被りがないならば（互いに素）

\displaystyle \begin{eqnarray} P \left( \bigcup_{n=1}^{\infty} A_n \right) = \sum_{n=1}^{\infty} P(A_n) \end{eqnarray}

が成り立つ。つまり、全体の確率は、各々の確率の和に等しい

最後の性質は完全加法性と呼ばれている重要なものです。以上の性質を満たす関数を確率測度と呼び、この関数に対して事象（集合）を入力したときに出力される値を確率と呼びます。

このように、ぎりぎりのところまで事象と確率を拡張しておくと応用上役に立つのです。以上は必要条件だけで、どのように確率を割り当てるかはまた別の問題です。

事象のことを可測集合とも呼びます。これは読んで字の如く、「測れる集合」です。測れる集合とは前に述べたような条件を満たす集合のことです。全事象 \Omega と事象の集合 \mathscr{F} のペアを可測空間と呼びます。全事象の中に、測れる集合、すなわち事象の集合を設定したわけです。事象の集合には色々な取り方があります。それが例 2.1.4です。

可測空間に確率測度 P を組み合わせた3つ組み (\Omega, \mathscr{F}, P) を確率空間と呼ぶ、というのが定義 2.1.6です。つまり、全事象を用意して、測れる集合、すなわち事象を決めて、それに対して確率を割り振る関数、確率測度を決めてやってはじめて確率というものが考えられるということです。

定義 2.1.7は、確率を与えない集合が存在する、ということを言っています。測度が零の集合（零集合）ということです。

ある事象が起きる確率が1であるとき、その事象はほとんど確実に（almost surely、almost certainly）起きる、と呼びます。これが定義 2.1.8で、なぜ「ほとんど確実」かというと、測度が0の集合を事象として考えていないからです。

零集合の部分集合は必ずしも事象になっていません。しかし、これらが事象であるとき、この確率空間を完備であると呼びます。完備であるかどうかは起きる確率が0の集合にしか影響しないので、実用上は完備で無くとも問題ないようです。しかし、数学的に可測空間や確率空間で様々な列の極限を考える際には、完備でないと困ります。完備でないときは完備化という手法で完備にできます。たしか、列の極限を集合に加える、という操作だったと思います。なので、確率空間ははじめから完備であると仮定してよいのです。


【確率過程】第1章「さまざまな応用分野における確率微分方程式」

数学 最適制御 確率論 確率過程 解析学

兼清泰明 著『確率微分方程式とその応用』を読んでいきます。今回は第1章「さまざまな応用分野における確率微分方程式」を読みます。

確率微分方程式とその応用

確率微分方程式とその応用

第1章「さまざまな応用分野における確率微分方程式」


確率微分方程式とはどのようなものか、そしてどのように応用されているか、という概要を学びました。