【有限体積法】1次元移流方程式をMUSCL法で解く C++コード付き
今回は1次元移流方程式を1次の風上差分+MUSCL法で解いていきます。MUSCL法とは、セル内で一定だった未知数のプロファイルを1次以上の関数で補外しセル界面での値を計算し、その値を用いて数値流速を計算することによって高次精度を達成する方法です。その際に、数値振動が発生しないように勾配制限関数(slope limiter)が用いられます。今回はminmod関数を使いました。
1次元移流方程式とは
のような一階の偏微分方程式のことをいいます。ここで、 は溶質の濃度、
は風などによる移流速度です。
今回の計算条件は、移流速度が正 で、初期条件は領域の左端の矩形波(長方形の波)です。比較のために普通の風上差分で解いた結果も載せます。
これが計算結果です。青がMUSCLで、赤が1次の風上差分です。
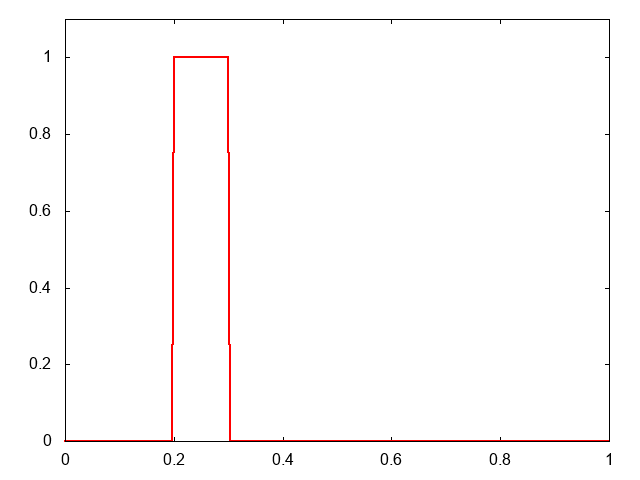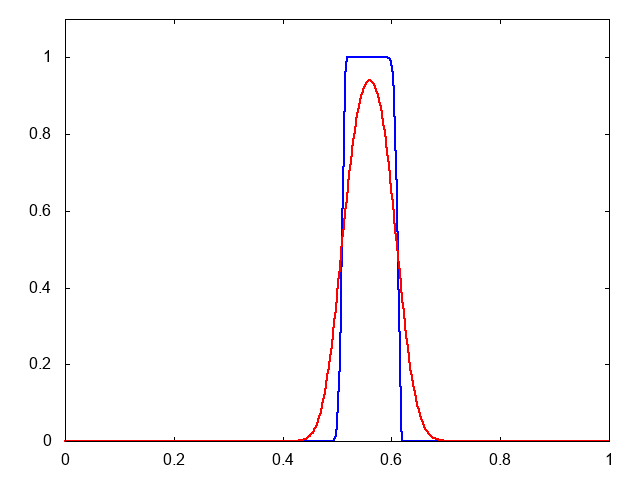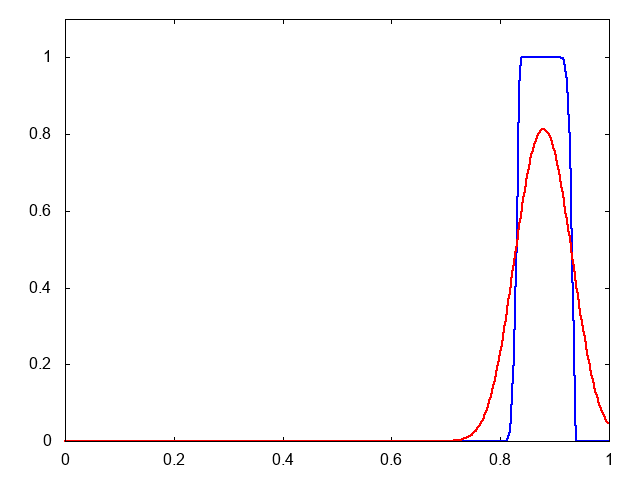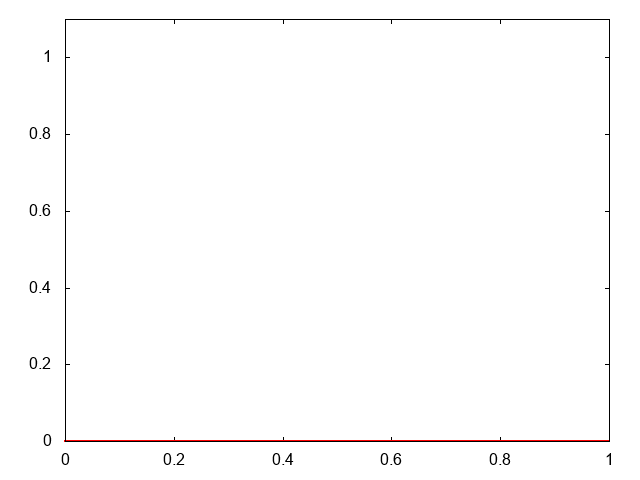
MUSCLのほうが初期プロファイルをよく保っているのがわかります。また、1次の風上差分の数値粘性の大きさもわかります。こんなに拡散されているのですね。
では、計算コードです。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; //flux for advection equation// inline double Fluxadv(double V, double uL, double uR) { return max(V,0.0)*uL-max(-V,0.0)*uR; } //flux limiter minmod// inline double minmod(double d1, double d2) { if(d1*d2<=0) { return 0.0; } else if(abs(d1)<abs(d2)) { return d1; } else { return d2; } } //reconstruction// inline void reconst(int Node, double dt, double dx, double u[], double uiL[], double uiR[]) { //inner cells// for(int i=1;i<Node-1;i++) { //jump// double dul=u[i]-u[i-1]; double dur=u[i+1]-u[i]; //slope with slope limiter// double k=0.0; double b=(3.0-k)/(1.0-k); double dulLim=minmod(dur,b*dul); double durLim=minmod(dul,b*dur); double delu=(1.0+k)/2.0*dulLim+(1.0-k)/2.0*durLim; //boundary extrapolation// uiL[i]=u[i]-0.5*delu; uiR[i]=u[i]+0.5*delu; } //BC// //i=0// uiL[0]=uiL[1]; uiR[0]=uiR[1]; //i=Node-1// uiL[Node-1]=uiL[Node-2]; uiR[Node-1]=uiR[Node-2]; } inline void output(double u[], int Node, double dx) { stringstream ss; string name; ofstream fo; static int count=0; ss<<count; name=ss.str(); name="u_" + name + ".txt"; fo.open(name.c_str ()); for(int i=0;i<Node;i++) { fo<<dx*float(i)<<" "<<u[i]<<endl; } fo<<endl; fo<<endl; count+=1; } int main() { const int Cell=400; const int Node=Cell+1; int div=100;//for output double LL=1.0; double dx=LL/(Node-1); double dt=0.001; double TotalTime=10; double V=0.1; double u[Node]; double ub[Node]; double un[Node]; double FL; double FR; double uiL[Node]; double uiR[Node]; //IC// for(int i=0;i<Node;i++) { u[i]=0.0; if((i>=80)&&(i<=120)) u[i]=1.0; } //IC output// output(u,Node,dx); //time step// for(int k=1;double(k)*dt<=TotalTime;k++) { //reconstruction// reconst(Node,dt,dx,u,uiL,uiR); //inner cells// for(int i=1;i<Node-1;i++) { //FR=Fluxadv(V,u[i],u[i+1]); //FL=Fluxadv(V,u[i-1],u[i]); FR=Fluxadv(V,uiR[i],uiL[i+1]); FL=Fluxadv(V,uiR[i-1],uiL[i]); un[i]=u[i]-dt/dx*(FR-FL); } //BC// //left boundary// un[0]=un[1]; //right boundary// un[Node-1]=un[Node-2]; //update// for(int i=0;i<Node;i++) { u[i]=un[i]; } //output// if(k%div==0) { output(u,Node,dx); cout<<"t="<<double(k)*dt<<endl; } } return 0; }
こちらではToro流のslope limiterを入れてあります。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; //flux for advection equation// inline double Fluxadv(double V, double uL, double uR) { return max(V,0.0)*uL-max(-V,0.0)*uR; } //flux limiter superbee// inline double superbee(double d1, double d2, double delta, double omega) { double zeta; if(d1*d2<=0) { zeta=0.0; } else { if(d1/d2<=0.5) { zeta=2.0*d1/d2; } else if(d1/d2<=1.0) { zeta=1.0; } else { double zetaR=2.0/(1.0-omega+(1.0+omega)*d1/d2); zeta=min(zetaR,d1/d2); zeta=min(zeta,2.0); } } return zeta*delta; } //reconstruction// inline void reconst(int Node, double dt, double dx, double u[], double uiL[], double uiR[]) { //inner cells// for(int i=1;i<Node-1;i++) { //jump// double dul=u[i]-u[i-1]; double dur=u[i+1]-u[i]; //slope// double omega=0.0; double delu=(1.0+omega)/2.0*dul+(1.0-omega)/2.0*dur; //slope limiter// delu=superbee(dul,dur,delu,omega); //boundary extrapolation// uiL[i]=u[i]-0.5*delu; uiR[i]=u[i]+0.5*delu; } //BC// //i=0// uiL[0]=uiL[1]; uiR[0]=uiR[1]; //i=Node-1// uiL[Node-1]=uiL[Node-2]; uiR[Node-1]=uiR[Node-2]; } inline void output(double u[], int Node, double dx) { stringstream ss; string name; ofstream fo; static int count=0; ss<<count; name=ss.str(); name="u_" + name + ".txt"; fo.open(name.c_str ()); for(int i=0;i<Node;i++) { fo<<dx*float(i)<<" "<<u[i]<<endl; } fo<<endl; fo<<endl; count+=1; } int main() { const int Cell=800; const int Node=Cell+1; int div=100;//for output double LL=1.0; double dx=LL/(Node-1); double dt=0.001; double TotalTime=10; double V=0.1; double u[Node]; double ub[Node]; double un[Node]; double FL; double FR; double uiL[Node]; double uiR[Node]; //IC// for(int i=0;i<Node;i++) { u[i]=0.0; if((i>=80)&&(i<=160)) u[i]=1.0; } //IC output// output(u,Node,dx); //time step// for(int k=1;double(k)*dt<=TotalTime;k++) { //reconstruction// reconst(Node,dt,dx,u,uiL,uiR); //inner cells// for(int i=1;i<Node-1;i++) { //FR=Fluxadv(V,u[i],u[i+1]); //FL=Fluxadv(V,u[i-1],u[i]); FR=Fluxadv(V,uiR[i],uiL[i+1]); FL=Fluxadv(V,uiR[i-1],uiL[i]); un[i]=u[i]-dt/dx*(FR-FL); } //BC// //left boundary// un[0]=un[1]; //right boundary// un[Node-1]=un[Node-2]; //update// for(int i=0;i<Node;i++) { u[i]=un[i]; } //output// if(k%div==0) { output(u,Node,dx); cout<<"t="<<double(k)*dt<<endl; } } return 0; }