【差分法】SMAC法で3次精度風上差分を用いてNavier-Stokes方程式を解きました C++コード付き
SMAC法(Simplified Maker And Cell method)で3次精度風上差分を用いてNavier-Stokes方程式を数値的に解いてみました。今回は高次の風上差分を入れてみました。以下も参照してください。
離散化は以下を見てください。河村哲也著『流体解析の基礎』のpp.71-74も非常に参考になります。3次精度風上差分は今後まとめます。

- 作者: 河村哲也
- 出版社/メーカー: 朝倉書店
- 発売日: 2014/03/26
- メディア: 単行本
- この商品を含むブログ (1件) を見る
計算条件ですが、正方形のサイズは1×1、上部の壁は右へ速さ1で移動、節点数は31×31、セル数は30×30、レイノルズ数は100であるとしています。
計算結果です。
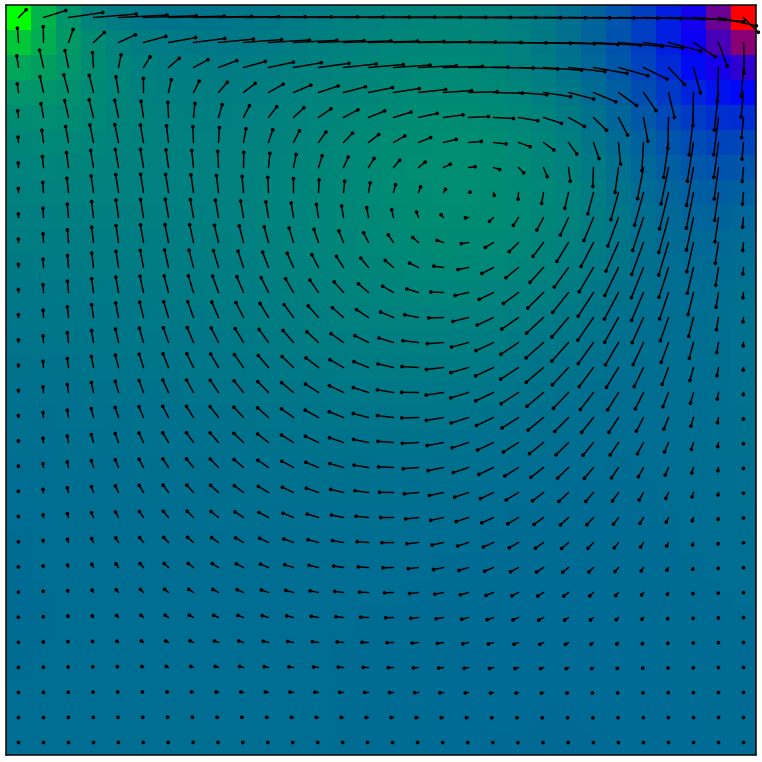
グラデーションが圧力をあらわしています。緑が圧力が小さい、青が中間、赤が圧力が高いことをあらわしています。黒い線は各セルにおける流速ベクトルを示しています。黒い丸が付いている方向へと流れています。黒い丸だけの所は流れが無いと考えて下さい。1次の風上差分の結果と比べてみてください。
ではコードです。端は1次の風上差分で計算しています。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; inline void update(int xn, int yn, double &dx, double &dy, double &dt, double u[], double v[], double p[], double dp[], double &divv, double &uwall) { int i,j; //u// for(i=2;i<xn;i++) { for(j=1;j<yn;j++) { u[i*(yn+1)+j]=u[i*(yn+1)+j]+dt*(dp[(i-1)*(yn+1)+j]-dp[i*(yn+1)+j])/dx; } } //v// for(i=1;i<xn;i++) { for(j=2;j<yn;j++) { v[i*(yn+2)+j]=v[i*(yn+2)+j]+dt*(dp[i*(yn+1)+j-1]-dp[i*(yn+1)+j])/dy; } } //p// for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { p[i*(yn+1)+j]=p[i*(yn+1)+j]+dp[i*(yn+1)+j]; } } divv=0.; for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { divv+=fabs((u[(i+1)*(yn+1)+j]-u[i*(yn+1)+j])/dx+(v[i*(yn+2)+j+1]-v[i*(yn+2)+j])/dy); } } } inline void poi(int &km, int xn, int yn, double &dx, double &dy, double &dt, double dp[], double &err, double &re, double u[], double v[]) { int i,j,k; double C1=dy*dy/(2.0*(dx*dx+dy*dy)); double C2=dx*dx/(2.0*(dx*dx+dy*dy)); double C3=dx*dx*dy*dy/(2.0*(dx*dx+dy*dy))/dt; double in; //initialization// for(i=0;i<xn+1;i++) { for(j=0;j<yn+1;j++) { dp[i*(yn+1)+j]=0.; } } //Poisson equation// for(k=1;k<=km;k++) { err=0.; //Neumann BC// for(j=0;j<yn+1;j++) { dp[0*(yn+1)+j]=dp[1*(yn+1)+j]; dp[xn*(yn+1)+j]=dp[(xn-1)*(yn+1)+j]; } for(i=0;i<xn+1;i++) { dp[i*(yn+1)+0]=dp[i*(yn+1)+1]; dp[i*(yn+1)+yn]=dp[i*(yn+1)+yn-1]; } //iteration// for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { in=dp[i*(yn+1)+j]; dp[i*(yn+1)+j]=C1*(dp[(i+1)*(yn+1)+j]+dp[(i-1)*(yn+1)+j])+C2*(dp[i*(yn+1)+j+1]+dp[i*(yn+1)+j-1])-C3*((u[(i+1)*(yn+1)+j]-u[i*(yn+1)+j])/dx+(v[i*(yn+2)+j+1]-v[i*(yn+2)+j])/dy); err+=(dp[i*(yn+1)+j]-in)*(dp[i*(yn+1)+j]-in); } } if(err<=0.001) break; } } inline void u1upwind(int i, int j, int yn, double &dx, double &dy, double &dt, double u[], double v[], double p[], double &re) { double udif; double vmid; double uux,vuy,uvx,vvy; if(u[i*(yn+1)+j]>=0) { uux=u[i*(yn+1)+j]*(u[(i+1)*(yn+1)+j]-u[i*(yn+1)+j])/dx; } else { uux=u[i*(yn+1)+j]*(u[i*(yn+1)+j]-u[(i-1)*(yn+1)+j])/dx; } vmid=(v[i*(yn+2)+j]+v[i*(yn+2)+j+1]+v[(i-1)*(yn+2)+j+1]+v[(i-1)*(yn+2)+j])/4.0; if(vmid>=0) { vuy=vmid*(u[i*(yn+1)+j+1]-u[i*(yn+1)+j])/dy; } else { vuy=vmid*(u[i*(yn+1)+j]-u[i*(yn+1)+j-1])/dy; } udif=(u[(i+1)*(yn+1)+j]-2.0*u[i*(yn+1)+j]+u[(i-1)*(yn+1)+j])/dx/dx+(u[i*(yn+1)+j+1]-2.0*u[i*(yn+1)+j]+u[i*(yn+1)+j-1])/dy/dy; u[i*(yn+1)+j]=u[i*(yn+1)+j]+dt*(-uux-vuy-(p[i*(yn+1)+j]-p[(i-1)*(yn+1)+j])/dx+1.0/re*udif); } inline void v1upwind(int i, int j, int yn, double &dx, double &dy, double &dt, double u[], double v[], double p[], double &re) { double vdif; double umid; double uux,vuy,uvx,vvy; umid=(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j]+u[(i+1)*(yn+1)+j-1]+u[i*(yn+1)+j-1])/4.0; if(umid>=0) { uvx=umid*(v[(i+1)*(yn+2)+j]-v[i*(yn+2)+j])/dx; } else { uvx=umid*(v[i*(yn+2)+j]-v[(i-1)*(yn+2)+j])/dx; } if(v[i*(yn+2)+j]>=0) { vvy=v[i*(yn+2)+j]*(v[i*(yn+2)+j+1]-v[i*(yn+2)+j])/dy; } else { vvy=v[i*(yn+2)+j]*(v[i*(yn+2)+j]-v[i*(yn+2)+j-1])/dy; } vdif=(v[(i+1)*(yn+2)+j]-2.0*v[i*(yn+2)+j]+v[(i-1)*(yn+2)+j])/dx/dx+(v[i*(yn+2)+j+1]-2.0*v[i*(yn+2)+j]+v[i*(yn+2)+j-1])/dy/dy; v[i*(yn+2)+j]=v[i*(yn+2)+j]+dt*(-uvx-vvy-(p[i*(yn+1)+j]-p[i*(yn+1)+j-1])/dy+1.0/re*vdif); } inline void u3upwind(int i, int j, int yn, double &dx, double &dy, double &dt, double u[], double v[], double p[], double &re) { double udif; double vmid; double uux,vuy,uvx,vvy; if(u[i*(yn+1)+j]>=0) { uux=u[i*(yn+1)+j]*(2.0*u[(i+1)*(yn+1)+j]+3.0*u[i*(yn+1)+j]-6.0*u[(i-1)*(yn+1)+j]+1.0*u[(i-2)*(yn+1)+j])/dx/6.0; } else { uux=u[i*(yn+1)+j]*(-1.0*u[(i+2)*(yn+1)+j]+6.0*u[(i+1)*(yn+1)+j]-3.0*u[i*(yn+1)+j]-2.0*u[(i-1)*(yn+1)+j])/dx/6.0; } vmid=(v[i*(yn+2)+j]+v[i*(yn+2)+j+1]+v[(i-1)*(yn+2)+j+1]+v[(i-1)*(yn+2)+j])/4.0; if(vmid>=0) { vuy=vmid*(2.0*u[i*(yn+1)+j+1]+3.0*u[i*(yn+1)+j]-6.0*u[i*(yn+1)+j-1]+1.0*u[i*(yn+1)+j-2])/dy/6.0; } else { vuy=vmid*(-1.0*u[i*(yn+1)+j+2]+6.0*u[i*(yn+1)+j+1]-3.0*u[i*(yn+1)+j]-2.0*u[i*(yn+1)+j-1])/dy/6.0; } udif=(u[(i+1)*(yn+1)+j]-2.0*u[i*(yn+1)+j]+u[(i-1)*(yn+1)+j])/dx/dx+(u[i*(yn+1)+j+1]-2.0*u[i*(yn+1)+j]+u[i*(yn+1)+j-1])/dy/dy; u[i*(yn+1)+j]=u[i*(yn+1)+j]+dt*(-uux-vuy-(p[i*(yn+1)+j]-p[(i-1)*(yn+1)+j])/dx+1.0/re*udif); } inline void v3upwind(int i, int j, int yn, double &dx, double &dy, double &dt, double u[], double v[], double p[], double &re) { double vdif; double umid; double uux,vuy,uvx,vvy; umid=(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j]+u[(i+1)*(yn+1)+j-1]+u[i*(yn+1)+j-1])/4.0; if(umid>=0) { uvx=umid*(2.0*v[(i+1)*(yn+2)+j]+3.0*v[i*(yn+2)+j]-6.0*v[(i-1)*(yn+2)+j]+1.0*v[(i-2)*(yn+2)+j])/dx/6.0; } else { uvx=umid*(-1.0*v[(i+2)*(yn+2)+j]+6.0*v[(i+1)*(yn+2)+j]-3.0*v[i*(yn+2)+j]-2.0*v[(i-1)*(yn+2)+j])/dx/6.0; } if(v[i*(yn+2)+j]>=0) { vvy=v[i*(yn+2)+j]*(2.0*v[i*(yn+2)+j+1]+3.0*v[i*(yn+2)+j]-6.0*v[i*(yn+2)+j-1]+1.0*v[i*(yn+2)+j-2])/dy/6.0; } else { vvy=v[i*(yn+2)+j]*(-1.0*v[i*(yn+2)+j+2]+6.0*v[i*(yn+2)+j+1]-3.0*v[i*(yn+2)+j]-2.0*v[i*(yn+2)+j-1])/dy/6.0; } vdif=(v[(i+1)*(yn+2)+j]-2.0*v[i*(yn+2)+j]+v[(i-1)*(yn+2)+j])/dx/dx+(v[i*(yn+2)+j+1]-2.0*v[i*(yn+2)+j]+v[i*(yn+2)+j-1])/dy/dy; v[i*(yn+2)+j]=v[i*(yn+2)+j]+dt*(-uvx-vvy-(p[i*(yn+1)+j]-p[i*(yn+1)+j-1])/dy+1.0/re*vdif); } inline void vel(int xn, int yn, double u[], double v[], double &dx, double &dy, double &dt, double p[], double &re, double &uwall) { int i,j; double udif,vdif; double umid,vmid; double uux,vuy,uvx,vvy; //BC for left and right// for(j=0;j<yn+1;j++) { u[1*(yn+1)+j]=0.; u[0*(yn+1)+j]=u[2*(yn+1)+j]; v[0*(yn+2)+j]=-v[1*(yn+2)+j]; u[xn*(yn+1)+j]=0.; u[(xn+1)*(yn+1)+j]=u[(xn-1)*(yn+1)+j]; v[xn*(yn+2)+j]=-v[(xn-1)*(yn+2)+j]; } v[0*(yn+2)+yn+1]=-v[1*(yn+2)+yn+1]; v[xn*(yn+2)+yn+1]=-v[(xn-1)*(yn+2)+yn+1]; //BC for bottom and top// for(i=0;i<xn+1;i++) { v[i*(yn+2)+1]=0.; v[i*(yn+2)+0]=v[i*(yn+2)+2]; u[i*(yn+1)+0]=-u[i*(yn+1)+1]; v[i*(yn+2)+yn]=0.; v[i*(yn+2)+yn+1]=v[i*(yn+2)+yn-1]; u[i*(yn+1)+yn]=2.0*uwall-u[i*(yn+1)+yn-1];//for wall } u[(xn+1)*(yn+1)+0]=-u[xn*(yn+1)+0]; u[(xn+1)*(yn+1)+yn]=-u[xn*(yn+1)+yn]; //Neumann BC// for(j=0;j<yn+1;j++) { p[0*(yn+1)+j]=p[1*(yn+1)+j]; p[xn*(yn+1)+j]=p[(xn-1)*(yn+1)+j]; } for(i=0;i<xn+1;i++) { p[i*(yn+1)+0]=p[i*(yn+1)+1]; p[i*(yn+1)+yn]=p[i*(yn+1)+yn-1]; } //u// for(i=2;i<xn;i++) { //1st order upwind// j=1; u1upwind(i,j,yn,dx,dy,dt,u,v,p,re); j=yn-1; u1upwind(i,j,yn,dx,dy,dt,u,v,p,re); for(j=2;j<yn-1;j++) { //3rd order upwind// u3upwind(i,j,yn,dx,dy,dt,u,v,p,re); } } //v// for(j=2;j<yn;j++) { //1st order upwind// i=1; v1upwind(i,j,yn,dx,dy,dt,u,v,p,re); i=xn-1; v1upwind(i,j,yn,dx,dy,dt,u,v,p,re); for(i=2;i<xn-1;i++) { //3rd order upwind// v3upwind(i,j,yn,dx,dy,dt,u,v,p,re); } } } int main() { const int xn=31; const int yn=31; int i,j,l; double divv; double err; double *u=new double[(xn+2)*(yn+1)]; double *v=new double[(xn+1)*(yn+2)]; double *p=new double[(xn+1)*(yn+1)]; double *dp=new double[(xn+1)*(yn+1)]; double uwall=1.; double dx=1./(double)(xn-1); double dy=1./(double)(yn-1); double dt=0.001; double re=100; int lm=20000; int km=100; ofstream fk,ff; fk.open("vel.txt"); ff.open("pre.txt"); //initialization// for(i=0;i<xn+1;i++) { for(j=0;j<yn+1;j++) { p[i*(yn+1)+j]=0.; dp[i*(yn+1)+j]=0.; } } for(i=0;i<xn+2;i++) { for(j=0;j<yn+1;j++) { u[i*(yn+1)+j]=0.; } } for(i=0;i<xn+1;i++) { for(j=0;j<yn+2;j++) { v[i*(yn+2)+j]=0.; } } //time step// for(l=1;l<=lm;l++) { vel(xn,yn,u,v,dx,dy,dt,p,re,uwall); poi(km,xn,yn,dx,dy,dt,dp,err,re,u,v); update(xn,yn,dx,dy,dt,u,v,p,dp,divv,uwall); if(l%1000==0) cout<<l<<" "<<err<<" "<<divv<<endl; } //output for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { fk<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j])/2.0<<" "<<(v[i*(yn+2)+j]+v[i*(yn+2)+j+1])/2.0<<endl; ff<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<p[i*(yn+1)+j]<<endl; } } delete[] u,v,p,dp; return 0; }