【有限要素法】1次元定常移流拡散方程式をGalerkin法で解く C++コード付き

今回は1次元定常移流拡散方程式を有限要素法（Galerkin法）で解いていきます。C++コード付きです。1次元定常移流拡散方程式は、前に書いた記事「有限要素法のプログラミングを勉強するときにどの順序で学ぶのがよいか？」で紹介した、有限要素法を学ぶ場合に二番目に解くべき方程式です。ただし今回は風上化は入れていません。

1次元定常移流拡散方程式とは

のような二階の常微分方程式のことをいいます。ここで、 は溶質の濃度、 は風などによる移流速度、 は拡散の効果を表す拡散係数と解釈することができます。ある溶質が移流や拡散のもとでどのような分布をとるか求めるのがこの問題です。

前回の一次元Poisson方程式に移流行列を加えるだけなので簡単です。今境界条件は前回と同じく3パターン用意しました。すなわち、

Case 1, と でDirichlet条件を課す
（ と の値を指定）
Case 2, でNeumann条件、 でDirichlet条件を課す
（ と の値を指定）
Case 3, でDirichlet条件、 でNeumann条件を課す
（ と の値を指定）

です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。

コードです。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>

using namespace std;

//Gauss-Seidel//
inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps)
{
	int i,k;
	double in,sum,max;
	for(k=0;k<100000;k++)
	{
		max=0.0;
		in=x[0];
		
		for(i=0;i<Node;i++)
		{
			in=x[i];
			x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i];
			if(max<abs(in-x[i])) max=abs(in-x[i]);
		}
		
		if(eps>max) break;
	}
}

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double D[],double L[],double R[],double b[],double f[], int &Ele, double &dx, double &V, double &Diff)
{
	int i;
	for(i=0;i<Ele;i++)
	{
		//Diffusion//
		D[i]+=Diff/dx;R[i]+=-Diff/dx;
		L[i+1]+=-Diff/dx;D[i+1]+=Diff/dx;
		
		//Advection//
		D[i]+=-V/2.0;R[i]+=V/2.0;
		L[i+1]+=-V/2.0;D[i+1]+=V/2.0;
		
		//Source//
		b[i]+=(2.0*f[i]+1.0*f[i+1])*dx/6.0;
		b[i+1]+=(1.0*f[i]+2.0*f[i+1])*dx/6.0;
	}
}

inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node,double &Diff)
{
	if(bc==1)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
	}
	if(bc==2)
	{
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
		b[0]+=-N0*Diff;
	}
	if(bc==3)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		b[Node-1]+=N1*Diff;
	}
}

int main()
{
	int i;
	int Ele=100;
	int Node=Ele+1;
	double LL=1.0;
	double dx=LL/Ele;
	double eps=pow(2.0,-50);
	int bc=1;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=0.0;
	double D1=1.0; 
	double N0=0.0;
	double N1=2.0;
	double Diff=0.01;
	double V=0.1;
	double *b = new double[Node];
	double *x = new double[Node];
	double *f = new double[Node];
	double *D = new double[Node];
	double *L = new double[Node];
	double *R = new double[Node];

	for(i=0;i<Node;i++) 
	{
		b[i]=0.0;x[i]=0.0;f[i]=0.0;D[i]=0.0;L[i]=0.0;R[i]=0.0;
	}
	
	ofstream fk;
	fk.open("answer.txt");
	
	mat(D,L,R,b,f,Ele,dx,V,Diff);
	boundary(bc,D0,D1,N0,N1,D,L,R,b,Node,Diff);
	
	//Gauss-Seidel or TDMA//
	GS(D,L,R,x,b,Node,eps);
	//tdma(D,L,R,b,x,Node);
	
	for(i=0;i<Node;i++) cout<<x[i]<<endl;
	for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl;

	delete[] b,x,f,D,L,R;

	return 0;
}

計算結果を見てみましょう。

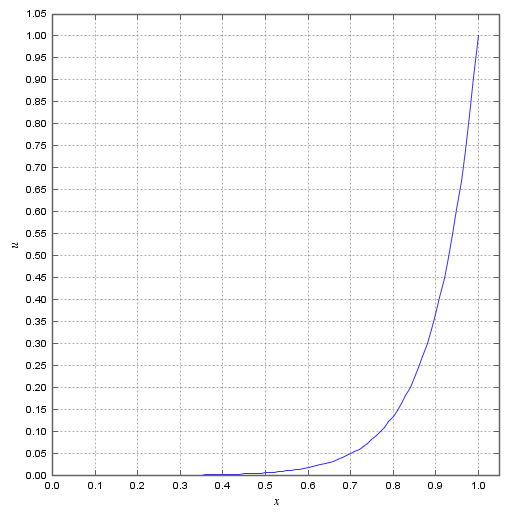
境界条件が正しく反映されていることを確認して下さい。移流の影響で全体的に右に寄っていることがわかります。

こちらの離散化も詳しく書く予定です。Galerkin法では移流が卓越する場合をきちんと扱えないので、移流方向を考慮した離散化「Petrov-Galerkin法」を使う必要があります。それも後程。書きたいこと、書かねばならぬことが山のようにあります。ひとつずつ着実に消化していきたいです。

【有限要素法】1次元Poisson方程式（ポアソン方程式）をGalerkin法で解く C++コード付き

今回は有限要素法の勉強で最初に解くであろう、1次元Poisson方程式を有限要素法（Galerkin法）で解くC++コードを公開します。前に書いた記事「有限要素法のプログラミングを勉強するときにどの順序で学ぶのがよいか？」で紹介した、有限要素法を学ぶ場合に、最初に解くべき方程式です。

普通のGalerkin法で離散化しています。二次元配列は一次元配列に収納しています。二次元配列を使ったほうが行列を足し合わせるときにわかりやすいので、初心者の方はそれでよいと思います。ただ要素数が増えてくると、二次元配列は重いので一次元配列のみで処理するのがおすすめです。

Poisson方程式とは

のような二階の偏微分方程式のことを言います。ここで は既知の関数です。1次元の場合は

となります。以下では とします。このとき解析解を求めることができます。

境界条件は3パターン扱うことができるようにつくってあります。すなわち、

Case 1, と でDirichlet条件を課す
（ と の値を指定）
Case 2, でNeumann条件、 でDirichlet条件を課す
（ と の値を指定）
Case 3, でDirichlet条件、 でNeumann条件を課す
（ と の値を指定）

です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。

コードです。今回は行列が三重対角行列になるので、配列のDに対角要素を、Lに対角要素の左隣の要素を、Rに対角要素の右隣の要素を格納しています。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>

using namespace std;

//Gauss-Seidel//
inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps)
{
	int i,k;
	double in,sum,max;
	for(k=0;k<100000;k++)
	{
		max=0.0;
		in=x[0];
		
		for(i=0;i<Node;i++)
		{
			in=x[i];
			x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i];
			if(max<abs(in-x[i])) max=abs(in-x[i]);
		}
		
		if(eps>max) break;
	}
}

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double D[],double L[],double R[],double b[],double f[], int &Ele, double &dx)
{
	int i;
	for(i=0;i<Ele;i++)
	{
		D[i]+=1.0/dx;R[i]+=-1.0/dx;
		L[i+1]+=-1.0/dx;D[i+1]+=1.0/dx;
		b[i]+=(2.0*f[i]+1.0*f[i+1])*dx/6.0;
		b[i+1]+=(1.0*f[i]+2.0*f[i+1])*dx/6.0;
	}
}

inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node)
{
	if(bc==1)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
	}
	if(bc==2)
	{
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
		b[0]+=-N0;
	}
	if(bc==3)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		b[Node-1]+=N1;
	}
}

int main()
{
	int i;
	int Ele=100;
	int Node=Ele+1;
	double LL=1.0;
	double dx=LL/Ele;
	double eps=pow(2.0,-50);
	int bc=3;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=1.0;
	double D1=2.0; 
	double N0=1.0;
	double N1=0.0;
	double *b = new double[Node];
	double *x = new double[Node];
	double *f = new double[Node];
	double *D = new double[Node];
	double *L = new double[Node];
	double *R = new double[Node];

	for(i=0;i<Node;i++) 
	{
		b[i]=0.0;x[i]=0.0;f[i]=1.0;D[i]=0.0;L[i]=0.0;R[i]=0.0;
	}
	
	ofstream fk;
	fk.open("answer.txt");
	
	mat(D,L,R,b,f,Ele,dx);
	boundary(bc,D0,D1,N0,N1,D,L,R,b,Node);
	
	//Gauss-Seidel or TDMA//
	//GS(D,L,R,x,b,Node,eps);
	tdma(D,L,R,b,x,Node);
	
	for(i=0;i<Node;i++) cout<<x[i]<<endl;
	for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl;

	delete[] b,x,f,D,L,R;

	return 0;
}

コードの流れですが、まず要素の分割数と境界条件の型（bcの値による）を決め、境界条件の設定（値をどうするか）を行い、関数 mat により行列を作成、関数 boundary で境界条件を行列に反映させ、関数 GS（Gauss-Seidel法）で作成した行列を解き、出力しています。出力はテキストファイル "answer.txt" に出てきます。左の行が 座標で右の行が求めている関数値 です。

それでは計算結果を見てみましょう。

きちんと境界条件が反映されているのがわかるでしょうか。左がDirichlet条件で値は1、右がNeumann条件で値は0です。

今回はコードがメインで離散化の詳細を示していませんが、必ず書くのでお待ちください。

【数値計算】Gauss-Seidel法（ガウス・ザイデル法）のC++コード

現在「【数値計算】Gauss-Seidel法（ガウス・ザイデル法）の説明　実践編」を準備中ですが、それに先立ってGauss-Seidel法のC++コードを公開します。私はコーディングの専門家ではないのであまり綺麗ではありませんが悪しからず。皆様の勉強に役立てて頂ければ幸いです。解いている問題は

で、答えは

となります。実際に動かして遊んでみて下さい。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <vector>

using namespace std;

//inner product//
inline double ip(vector<double> &a, vector<double> &b, int &size)
{
	double value=0.;
	int i;
	for(i=0;i<size;i++) value+=a[i]*b[i];
	return value;
}

//Gauss-Seidel
inline void GS(vector<vector<double> > &A,vector<double> &x,vector<double> &b, int &size, double &eps)
{
	int i,k;
	double in,sum,max;
	
	for(k=0;k<1000000;k++)
	{
		max=0.0;
		for(i=0;i<size;i++)
		{
			in=x[i];
			x[i]=(b[i]-(ip(A[i],x,size)-A[i][i]*x[i]))/A[i][i];
			if(max<abs(in-x[i])) max=abs(in-x[i]);
		}
		if(eps>max) break;
	}
}

int main()
{
	int size=3;
	int i;
	double eps=pow(2.0,-50);
	double in,max;
	vector<double> b(size,0.);
	vector<double> x(size,0.);
	vector<vector<double> > A(size,(vector<double>(size,0.)));
	
	A[0][0]=3;A[0][1]=2;A[0][2]=1;
	A[1][0]=1;A[1][1]=4;A[1][2]=1;
	A[2][0]=2;A[2][1]=2;A[2][2]=5;
	b[0]=10;b[1]=12;b[2]=21;
	
	GS(A,x,b,size,eps);

	for(i=0;i<size;i++) cout<<x[i]<<endl;

        return 0;
}

記事を書いていく順番について

ある事柄について書こうとすると、それを説明するための前提知識についても書かなくてはならなくなって、さらにその前提知識を説明するための前提知識についても書かなくてはならなくなって…、ときりがないのでこれからはどんどん書いていくことにします。もちろん、後で前提知識に関する記事を書いた場合はリンクを張る等していきます。あんまりしっかりやろうとして何も書けない状態よりは、多少がたがたしていてもどんどん書いていきます。

【数値計算】Gauss-Seidel法（ガウス・ザイデル法）の説明 理論編

Gauss-Seidel法とは

連立一次方程式を解くための基本的な反復法です。反復法とは一回の計算で解を求めるのではなく、ある決まった手順を何度も繰り返しながら真の解へと近づいていく方法です。数値計算では有限桁までしか表現できないので、得られる解は誤差を含んだものになります。ちなみに、何故連立一次方程式を解くのかというと、有限要素法などで方程式を離散化すると最終的に連立一次方程式に帰着されるからです。

反復手順

まず解こうとする連立一次方程式を

としましょう。ここで、 は の行列、 と は 次元のベクトルです。 と が既知で、 が未知です。例えば、 だと

です。この行列 を

と分解します。ここで、 は対角行列（対角成分以外は成分が0の行列）、 は下三角行列（対角線の下にだけ非零の成分が入っている行列）、 は上三角行列（対角線の上にだけ非零の成分が入っている行列）です。いかめしく書いていますが、具体例を見ればすぐ分かると思います。例えば、

としましょう。このとき、 は、

のように分解できるよね、と言っているだけです。さて、この分解を最初の連立一次方程式に代入すると

となります。次に、 を右辺に移項して

です。最後に、この両辺に の逆行列 を左からかけて

を得ます。これをもとにGauss-Seidel法の反復式を作ります。まず、 ステップ目での の近似解を としましょう。次のステップ（ ステップ目）での の近似解を先ほどの式を使って

のように決めることにします。これがGauss-Seidel法の反復式です。適当な初期値 からスタートした数列 は、もし収束するなら を満たす へと収束します。なぜなら、数列 が に収束したとすると

が成り立ちます。後はこの式を逆に変形していけば

となるので です。

実際の数値計算は有限桁なので、誤差が一定値以下になったら計算を切り上げます。誤差の決め方ですが、自分で決めた誤差の下限 （小さい値）に対して

となったら反復を止めることにします。この式の意味は、 ステップ目の近似解と ステップ目の近似解の差を取ったとき、その差が最大になるものが、あらかじめ定めておいた誤差の下限を下回ったら反復を止めるということです。つまり、近似解の値があまり更新されなくなったら反復を止めよう、と言っているだけです。実は他にも止める基準はあるのですがそれはまた今度。

長くなってきたので一度切りますが、これだけではきっと分からないと思うので、具体的な行列に対する例は次回書きます。

注　Gauss-Seidel法の収束については、結構大変なので別の記事で触れます。

参考

英語で学ぶ数値解析

楽しい反復法

【語学学習】どうやって新しい外国語を読めるようにするか？

私の外国語遍歴？

私は今までに色々な言語に手を出して参りました。大学での第二外学国語のアラビア語に始まり、ラテン語、ドイツ語、デンマーク語、オランダ語、古典ギリシャ語、フランス語、チェコ語、ロシア語、スペイン語、イタリア語。しかし、いろいろやりすぎて何も身に着かない状態が続いていました（それでも様々な言語に触れることが出来てよかったと思っていますが）。そこで、まずはひとつの言語をある程度までしっかり勉強してから他の言語に手を出すことにしました。そこで始めたのがドイツ語です。

文法を身につけましょう

ドイツ語を始めるにあたって、まずは薄い参考書を用いてその言語の全体をおおまかに把握することから始めました。あまり分厚い本に最初から取り組むと挫折しやすいので、最初は薄い参考書から始めましょう。この参考書をとにかく一度読み通します。活用や単語は、こんなのがあるんだ、ぐらいでどんどん進んでいきます。読み終えたらすぐに二週目を始めます。二回目は単語や活用をちゃんと覚えようと努力します。これで基礎文法は大丈夫だと思います。今まで私が語学学習を挫折してきたのはこの二週目の復習が無かったから、だと思います。一回読んだくらいだと人間どんどん忘れてしまいます。欲を言えば三週すれば万全でしょう。

単語もちゃんと覚えましょう

実は、今まで私が語学学習を挫折してきた理由はもう一つあるんです。それは、基礎的な単語を1000語以上覚える努力を完全に怠っていたのです。入門書を一周してだいたいのその言語の特徴を把握するだけで満足していたのです。それではいけません！単語集等を使って覚えましょう。千野栄一先生も著書の中で述べられているように、「語学で必要なのは語彙と文法」なのです。さらに、「基礎語を1000覚えてしまえば初級は卒業でその言語は無に戻ることはない」ということなのです。だから新しい外国語をやる時は、薄い文法書1冊と基礎語1000語を覚えることができる環境を作り出さないといけません。これは例えば、よいテキストや単語集、外国語に取り組む時間、そして気力ないしやる気です。

私のドイツ語は、文法書をやった後、"Mastering German Vocabulary"や『ドイツ基本語5000辞典』を使ってちゃんと単語を覚えたので（後者は10月に終わる予定）、辞書をひきひきWikipediaを読めるようになりました。これで初級は卒業です。初級を卒業したら他の外国語に手を出しても大丈夫です。今、私もフランス語をはじめています。

薄い参考書が終わったら、同じようなレベルの参考書を何冊か読む、のもオススメです。文法の復習にもなるし、場合によってはある本には載っていない文法事項を学習できたりします（入門書は意外とレベルがまちまちでどこまで載っている範囲が全然違う）。さらにここで未知語を拾っておくと1000語の壁を超えるのがかなり楽になります。

外国語上達法 (岩波新書 黄版 329)

Mastering German Vocabulary: A Thematic Approach (Barron's Vocabulary Series)

ドイツ基本語5000辞典

そして終わりのない中・上級へ

難しいのが中級からです。これはもうどんどん原文を読んでいくしかありません。なるべく自分の興味がある内容がよいです。Wikipediaはこのためにとても役に立ちます。あらかじめ日本語や英語でその記事を読んでおけば、ドイツ語の記事の内容が想像できます。類推もかなり効くようになります。しかも、専門性の高い記事ほど英語を訳しただけだったりするのでかなり読めます。さらに関連事項も読んでいくとよいです。Wikipediaを読みつつ、未知語を調べ暗記し、わからない文法事項は詳しめの文法書で調べて解決しましょう。やはり、読んでいて自然と出会う語彙がその人にとって本当に必要な語彙である、と思います。あと多少メジャーな言語だと中級向けの解釈の参考書や読本があるのでそれで学習しましょう。基本的に英語以外の言語の参考書はいつ絶版になってAmazonで高額で購入しないといけなくなるかわからないので積極的に入手していきましょう。私も将来やるであろう外国語の参考書を普段から集めています。趣味みたいなもんです。

注　新しい外国語は同時並行で2つ以上勉強しないほうがいいです。経験上どちらもポシャります。

【有限要素法】有限要素法のプログラミングを勉強するときにどの順序で学ぶのがよいか？【導入編】

有限要素法のプログラミングを勉強したいと思っている方はたくさんいると思います。私も最初はちんぷんかんぷんでした。Poisson方程式やら移流拡散方程式やらたくさん出てきます。有限要素法や数値計算の本を山ほど仕入れてきてうんうん唸っていました。そんな悪戦苦闘を通して、最近有限要素法がだんだんわかってきました。有限要素法を効率よく勉強するためには、以下の問題に対するプログラムを作成していくのが一番効率がよいと思います。

1次元Poisson方程式（1次元Laplace方程式でも可）
↓
1次元定常移流拡散方程式
↓
1次元非定常拡散方程式
↓
1次元非定常移流拡散方程式
↓
1次元非定常Burgers方程式

まずは1次元から始めるのがよいと思います。もちろん有限要素法が威力を発揮し始めるのは2次元以上ですがシンプルなものから勉強するべきです。

1次元Poisson方程式

そこで最初に1次元Poisson方程式を解くコードを作ります。これは拡散項のある定常問題を解けるようにするためです。ソース項のないLaplace方程式でも可です。ここで大規模な連立一次方程式の解法も学びます。私はGauss-Seidelを愛用していますが、Gaussの消去法も押さえておきましょう。TDMAでもokです。前者が反復法の代表で、後者が直接法の代表です。

1次元定常移流拡散方程式

この問題で拡散項と移流項が存在する定常問題の解き方を学びます。

1次元非定常拡散方程式

この問題では、拡散項だけが存在する非定常問題の解き方を学びます。陽解法、陰解法ともに作ります（ 法で離散化するとよいです）。

1次元非定常移流拡散方程式

次に非定常拡散方程式に移流項を足した問題の解き方を学びます。陽解法、陰解法ともに作ります。これが出来たら線型はもう大丈夫です。非線型問題を解くことは、線型問題を繰り返し解いていくのと同じなので線型問題が解けることは非常に重要です。

1次元非定常Burgers方程式

最後が1次元非定常Burgers方程式です。この問題では、非線型問題の解き方を学びます。Burgers方程式の場合は移流項が非線型項になります。将来Navier-Stokes方程式を解くときにも役立ちます。陽解法、陰解法ともに作ります。陰解法の場合は適当な反復法（Newton法とかPicard反復とか）が必要なのでそれも学びます。

導入なのでざっくりとしか書いていませんが流れはこんな感じです。このあとは風上化編に続きます（執筆中）。コードを書く際に参考になる文献の紹介や各問題の詳細な解説はまた別の記事でやります。

注　1次元移流方程式はリストに入れていませんが、これは風上化を導入した後に解くべきなのであとまわしになっています。