【有限要素法】1次元移流方程式をSUPG法で解く　C++コード付き

はじめに

今回は1次元移流方程式をSUPG（Stremline Upwind Petrov Galerkin）法で解いていきます。今までずっとやろうと思いながらも放置してきましたが、やっとやりました。

1次元移流方程式とは

$\displaystyle \frac{\partial u}{\partial t} + V\frac{\partial u}{\partial x} =0, \quad x \in [0, L]$

のような一階の偏微分方程式のことをいいます。ここで、 $u$ は溶質の濃度、 $V$ は風などによる移流速度です。

SUPG法とは？

SUPG法とは、有限要素法における風上化の一種です。Petrov Galerkin法とは、形状関数とは異なる重み関数を用いる有限要素法のことを言います。風上方向に重み関数を歪ませたのがSUPG法です。移流方程式にたいして通常のGalerkin法を適用すると数値振動が発生することから開発されました。

簡単に離散化を説明します（詳細な離散化は現在執筆中です）。行列で書くと

$\displaystyle (\boldsymbol{M} + \boldsymbol{M}_{\delta}) \boldsymbol{\dot{u}} + (\boldsymbol{S} + \boldsymbol{S}_{\delta}) \boldsymbol{u} = \boldsymbol{0}$

となります。ここで、 $\boldsymbol{M}$ が質量行列、 $\boldsymbol{S}$ が移流行列、 $\boldsymbol{M}_{\delta}$ が質量行列にたいするSUPG項、 $\boldsymbol{S}_{\delta}$ がにたいするSUPG項です。それぞれ、

$\displaystyle \boldsymbol{M}_{\delta} = \frac{1}{2} \tau V \left( \begin{array}{cc} -1 & 1 \\ -1 & 1 \\ \end{array} \right)$

$\displaystyle \boldsymbol{S}_{\delta} = \frac{1}{\Delta x} \tau V^2 \left( \begin{array}{cc} 1 & -1 \\ 1 & -1 \\ \end{array} \right)$

$\displaystyle \tau = \left( \left( \frac{2}{\Delta t} \right)^2 + \left( \frac{2 |V|}{\Delta x}^2 \right) \right)^{-\frac{1}{2}}$

のような形をしています。つまり、SUPG項は移流行列と拡散行列に適当な係数をかけた形になっています。なので、ガラーキン法で一度離散化していれば楽に計算できます。あとは時間項に対して適当な時間進行を入れればOKです。今回はオイラー法を使います（陰解法にすると数値振動を抑えられます）。

計算結果

今回の計算条件は、移流速度が正 $V=0.1$ で、初期条件は領域の左端の矩形波（長方形の波）です。以下が計算結果です。青が数値解です。

f:id:mutsumunemitsutan:20191025235015g:plain:w500

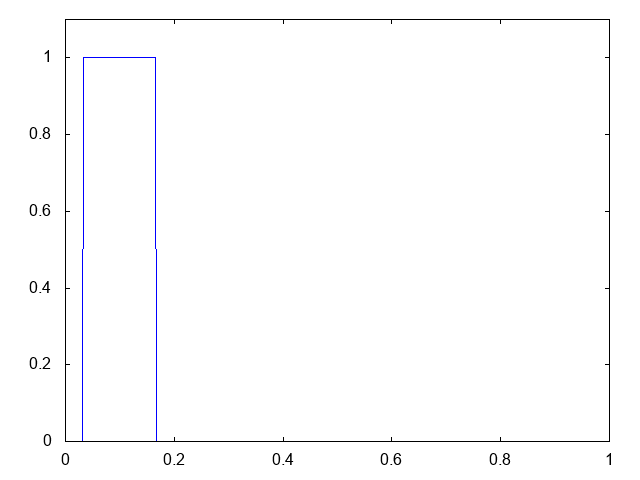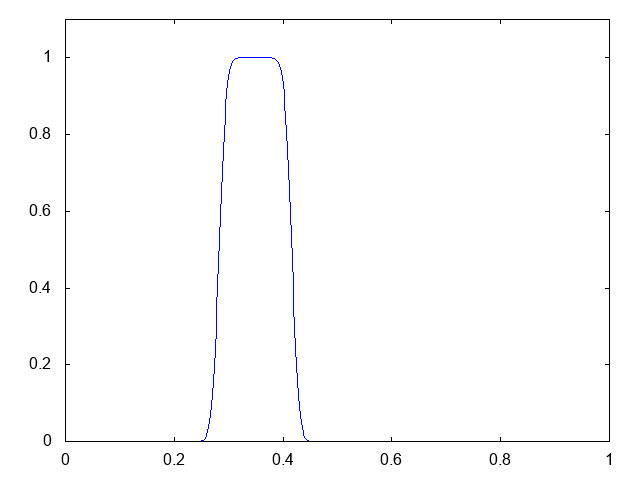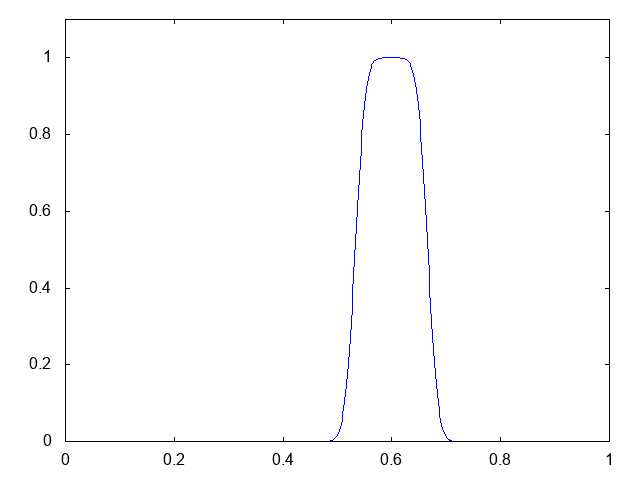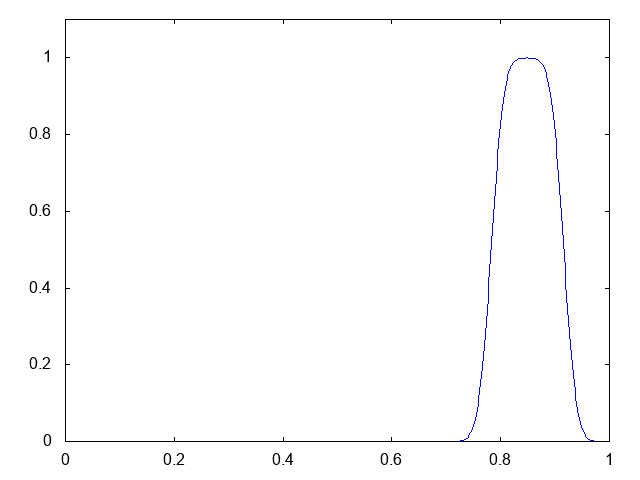
どうしても最初少し振動するのでコーディングが間違っているのかと思いましたが、どうやらSUPG法単体では、特に衝撃波面（勾配が急な箇所）で完全に振動を抑えられないようです。精度は有限体積法における1次風上差分と同じ、といった感触です。たしか、棚橋氏の本に、「SUPG法とは有限要素法における1次風上差分である」とった趣旨の記述があったと思います。SUPG法で振動を抑えるには別にリミターとか衝撃波補足項を入れる必要があるようです。SUPG法で移流方程式を計算した際にオーバーシュートとアンダーシュートが発生する、という記述が以下の論文にありました。みなさんもご注意下さい。彼らはリミター（カットオフ）を入れて対処しているようです。また、『計算力学』のp.184にある1次元移流方程式や『有限要素法による流れのシミュレーション』のp.56にある2次元移流方程式の例を見ても、オーバーシュートとアンダーシュートが発生しています。解が負にもなり得るというのは嫌ですね。解の非負性と離散最大値原理は満たしていてほしいです。

http://library.jsce.or.jp/jsce/open/00561/2005/3-24_3012f.pdf

C++コード

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <string>
#include <sstream>

using namespace std;

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double AD[],double AL[],double AR[],double BD[],double BL[],double BR[],double b[],double f[], int &Ele, double &dx, double &Diff, double &dt, double &V, int &Node)
{
	//initialization//
	for(int i=0;i<Node;i++)
	{
		AD[i]=0.0;AL[i]=0.0;AR[i]=0.0;BD[i]=0.0;BL[i]=0.0;BR[i]=0.0;
	}
	
	for(int i=0;i<Ele;i++)
	{
		double time=(2.0/dt);
		double advec=(2.0*abs(V)/dx);
		double tau=1.0/sqrt(time*time+advec*advec);
		
		double the=0.0;

		//A//
		//temporal//
		AD[i]+=dx*2.0/6.0/dt;
		AR[i]+=dx*1.0/6.0/dt;
		AL[i+1]+=dx*1.0/6.0/dt;
		AD[i+1]+=dx*2.0/6.0/dt;

		//SUPG for temporal//
		AD[i]+=-tau*V/2.0/dt;
		AR[i]+=tau*V/2.0/dt;
		AL[i+1]+=-tau*V/2.0/dt;
		AD[i+1]+=tau*V/2.0/dt;

		//advection//
        AD[i]+=the*-V/2.0;
		AR[i]+=the*V/2.0;
		AL[i+1]+=the*-V/2.0;
		AD[i+1]+=the*V/2.0;

		//SUPG for advection//
		AD[i]+=the*tau*V*V/dx;
		AR[i]+=-the*tau*V*V/dx;
		AL[i+1]+=the*-tau*V*V/dx;
		AD[i+1]+=the*tau*V*V/dx;
		
		//B//
		//temporal//
		BD[i]+=dx*2.0/6.0/dt;
		BR[i]+=dx*1.0/6.0/dt;
		BL[i+1]+=dx*1.0/6.0/dt;
		BD[i+1]+=dx*2.0/6.0/dt;

		//SUPG for temporal//
		BD[i]+=-tau*V/2.0/dt;
		BR[i]+=tau*V/2.0/dt;
		BL[i+1]+=-tau*V/2.0/dt;
		BD[i+1]+=tau*V/2.0/dt;
		
		//advection//
		BD[i]-=(1.0-the)*-V/2.0;
		BR[i]-=(1.0-the)*V/2.0;
		BL[i+1]-=(1.0-the)*-V/2.0;
		BD[i+1]-=(1.0-the)*V/2.0;

		//SUPG for advection//
		BD[i]-=(1.0-the)*tau*V*V/dx;
		BR[i]-=(1.0-the)*-tau*V*V/dx;
		BL[i+1]-=(1.0-the)*-tau*V*V/dx;
		BD[i+1]-=(1.0-the)*tau*V*V/dx;
	}
}

inline void boundary(int &bc,double AD[],double AL[],double AR[],double BD[],double BL[],double BR[],double b[],int &Node)
{
	if(bc==1)
	{
		AD[0]=1.0;AR[0]=0.0;BD[0]=1.0;BR[0]=0.0;
		AL[Node-1]=0.0;AD[Node-1]=1.0;BL[Node-1]=0.0;BD[Node-1]=1.0;
	}
	if(bc==2)
	{
		AL[Node-1]=0.0;AD[Node-1]=1.0;BL[Node-1]=0.0;BD[Node-1]=1.0;
	}
	if(bc==3)
	{
		AD[0]=1.0;AR[0]=0.0;BD[0]=1.0;BR[0]=0.0;
	}
}

inline void output(double x[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="answer_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*double(i)<<" "<<x[i]<<endl;
	}
	fo<<endl;
	
	count+=1;
}

int main()
{
	int i,j;
	int Ele=600;
	int Node=Ele+1;
	double LL=1.0;
	double dx=LL/Ele;
	double dt=0.001;
	double NT=1500;
	double eps=pow(2.0,-50);
	double Diff=0.01;
	double V=0.1;
	int bc=3;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=0.0;
	double D1=0.0;
	double N0=0.0;
	double N1=0.0;
    int div=5;
	
	double *b=new double[Node];
	double *x=new double[Node];
	double *xx=new double[Node];
	double *f=new double[Node];
	double *AD=new double[Node];
	double *AL=new double[Node];
	double *AR=new double[Node];
	double *BD=new double[Node];
	double *BL=new double[Node];
	double *BR=new double[Node];
	
	//initial condition//
	for(i=0;i<Node;i++)
	{
		x[i]=0.0;
	}

	for(i=20;i<100;i++)
	{
		x[i]=1.0;
	}

    output(x,Node,dx);
	mat(AD,AL,AR,BD,BL,BR,b,f,Ele,dx,Diff,dt,V,Node);
	boundary(bc,AD,AL,AR,BD,BL,BR,b,Node);
	
	for(i=1;i<=NT;i++)
	{
		//for b//
		if(bc==1)
		{
			b[0]=D0;
			b[Node-1]=D1;
		}
		if(bc==2)
		{
			b[Node-1]=D1;
			b[0]=BD[0]*x[0]+BR[0]*x[1]-N0*Diff;
		}
		if(bc==3)
		{
			b[0]=D0;
			b[Node-1]=BL[Node-1]*x[Node-2]+BD[Node-1]*x[Node-1]+N1*Diff;
		}
		
		for(j=1;j<Node-1;j++)
		{
			b[j]=BL[j]*x[j-1]+BD[j]*x[j]+BR[j]*x[j+1];
		}

		tdma(AD,AL,AR,b,xx,Node);
		for(j=0;j<Node;j++) x[j]=xx[j];
		
		if(i%div==0)
		{
			cout<<i<<endl;
			output(x,Node,dx);
		}
	}
	
	delete[] b,x,xx,f,AD,AL,AR,BD,BL,BR;
	
	return 0;
}

参考文献

最も参考にしたのが、『計算力学(第2版) 有限要素法の基礎』の第7章です。こちらは1次元移流方程式の例が載っています。この本は、有限要素法の入門書の中で一番読みやすい本だと思います。固体、流体ともに書いてある点が珍しいです。例が充実しており、離散化した際の行列の値が示されているので自分で離散化した結果と比べることができます。また、定常、非定常ともに載っているのもうれしいです。他には、『第3版有限要素法による流れのシミュレーション』の第3章を参考にしました。こちらは2次元移流方程式の例が載っています。