【浅水流方程式】MUSCL-Hancock法とHLL法でダム崩壊問題を解いてみました　動画とC++コード付き

【浅水流方程式】サイトマップ（ここから関連記事が探せます）
http://mathlang.hatenablog.com/entry/2018/12/18/213650

今回は、HLL法にMUSCL-Hancock法を組み合わせて高次精度化したスキームでダム崩壊問題を解きました。

普通のHLL法が時間・空間方向に対して1次精度なのにたいして、MUSCL-Hancock法を組み合わせたHLL法は、時間・空間方向に対して2次精度になります！普通のGodunov法（有限体積法）では各セルでの未知数は定数としますが、MUSCL-Hancock法では、各セルにおいて未知数は線型に変化するとします。こうすることにより、より高精度な数値流束を求めることが可能となります。また、衝撃波近傍での数値振動を回避するために、slope limiter（勾配制限関数）の一種であるsuperbee limiterを採用しています。

解いている方程式は、摩擦、勾配を無視した1次元浅水流方程式（Shallow Water Equations）です。

$\displaystyle \begin{eqnarray} &\frac{\partial h}{\partial t} + \frac{\partial q}{\partial x} = 0 \\ &\frac{\partial q}{\partial t} + \frac{\partial}{\partial x} \left( \frac{q^2}{h} + \frac{1}{2}gh^2 \right) = 0 \end{eqnarray}$

参考文献としてはToroの"Shock-Capturing Methods for Free-Surface Shallow Flows"のpp.205-210です。

Shock-Capturing Methods for Free-Surface Shallow Flows

作者: Eleuterio F. Toro
出版社/メーカー: Wiley
発売日: 2001/03/23
メディア: ハードカバー
この商品を含むブログを見る

こちらが計算結果です。青い線が水深です。

f:id:mutsumunemitsutan:20190706150338g:plain:w500

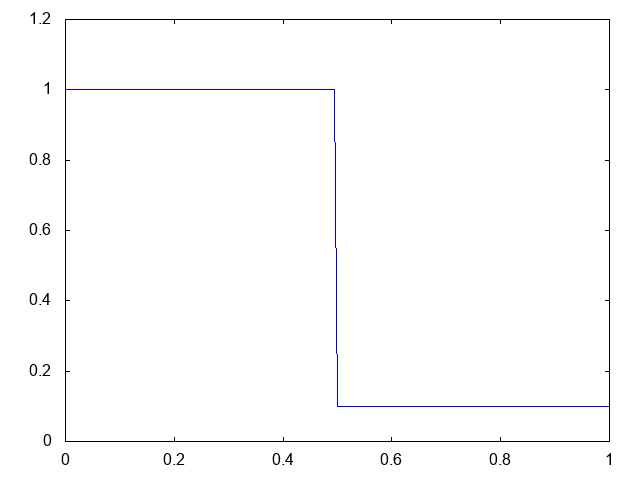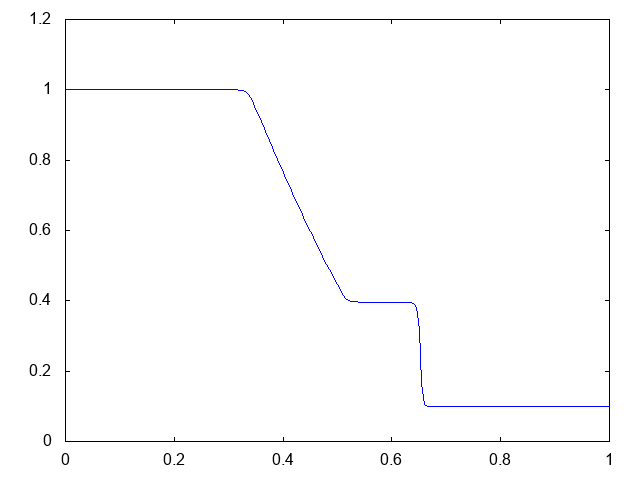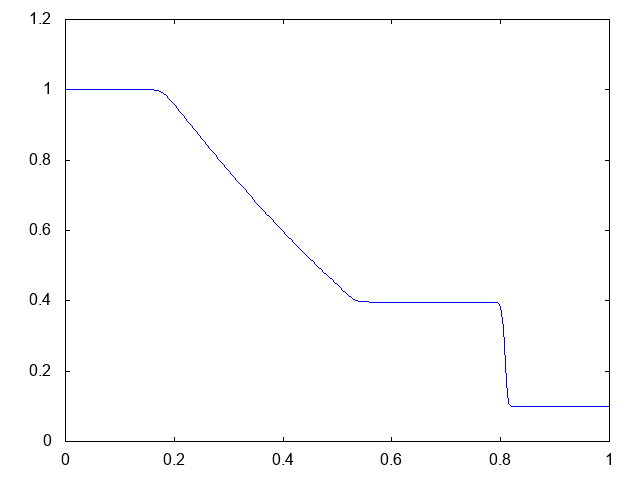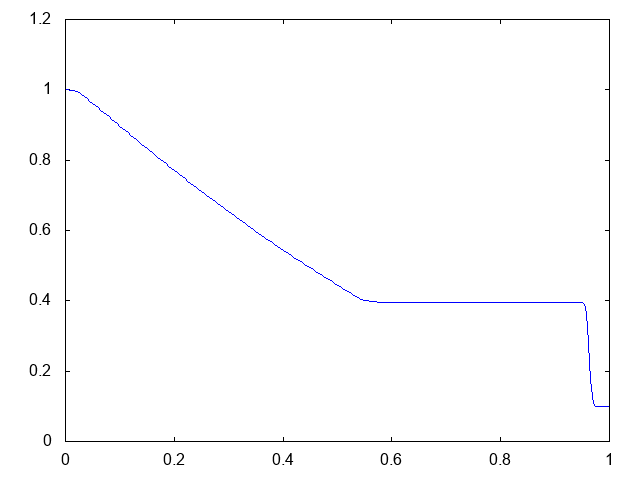
より少ない格子数で、普通のHLL法よりも衝撃波がシャープに捉えられています。

本当にそうだろうか？と疑問を持つ方のために比較動画を用意しました。セル数は100です。青がMUSCL-Hancock法を入れたHLL法で、赤がただのHLL法です。

f:id:mutsumunemitsutan:20190706155659g:plain:w500

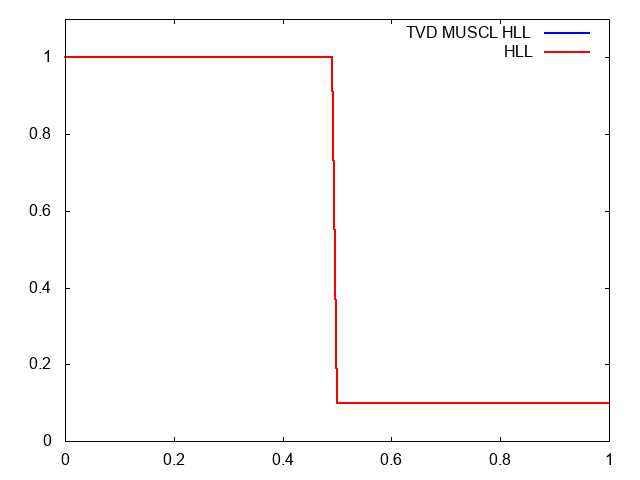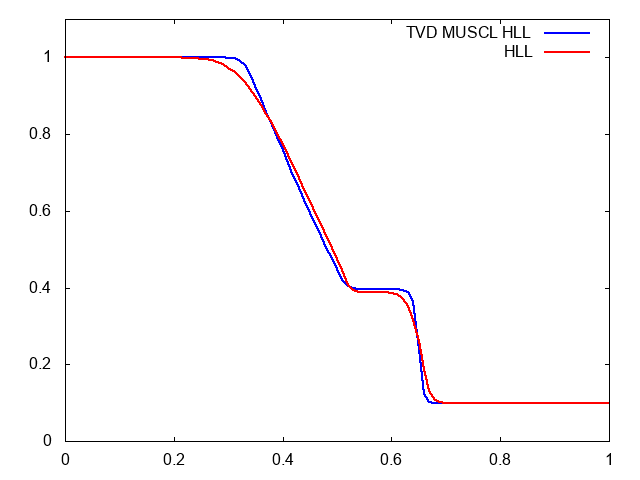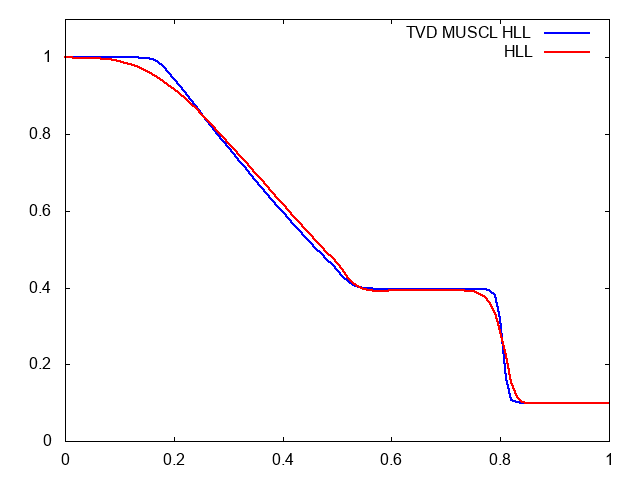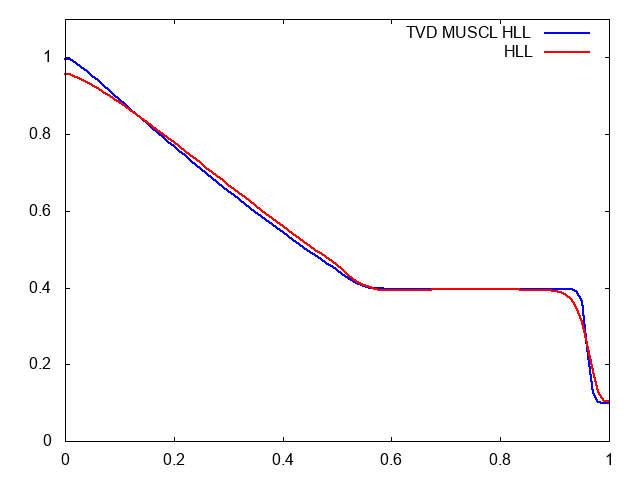
やはりMUSCLのほうが衝撃波の先端がシャープです。しかも、膨張波も角まで捉えられているし、途中の形状もより正確です。

では計算コードです。Toro流のslope limiterが入っています。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <sstream>

using namespace std;

const double g=9.8;

//celerity//
inline double a(double h)
{
	return sqrt(g*h);
}

//function for TRRS//
inline double gk(double h0, double hlr)
{
	return sqrt(g/2.0*(h0+hlr)/(h0*hlr));
}

//Riemann Solver Based on Exact Depth Positivity//
inline void EDPRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=(hL+hR)/2.0-(uR-uL)*(hL+hR)/4.0/(aL+aR);
	ust=(uL+uR)/2.0-(hR-hL)*(aL+aR)/(hL+hR);
}

//Two-Rarefaction Riemann Solver//
inline void TRRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=1.0/g*((aL+aR)/2.0+(uL-uR)/4.0)*((aL+aR)/2.0+(uL-uR)/4.0);
	ust=(uL+uR)/2.0+aL-aR;
}

//Two-Shock Riemann Solver//
inline void TSRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double uL=qL/hL;
	double uR=qR/hR;
	
	TRRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	double hcon=hst;
	hst=(gk(hst,hL)*hL+gk(hst,hR)*hR+uL-uR)/(gk(hst,hL)+gk(hst,hR));
	ust=(uL+uR)/2.0+((hcon-hR)*gk(hcon,hR)-(hcon-hL)*gk(hcon,hL))/2.0;
}

//function for HLL//
inline double qk(double hst, double hlr)
{
	double qk=1.0;
	if(hst>hlr) qk=sqrt((hst+hlr)*hst/(hlr*hlr)/2.0);
	return qk;
}


//left wave estimation//
inline double SLeft(double hst, double hL, double qL)
{
	double uL=qL/hL;
	return uL-a(hL)*qk(hst,hL);
}

//right wave estimation//
inline double SRight(double hst, double hR, double qR)
{
	double uR=qR/hR;
	return uR+a(hR)*qk(hst,hR);
}

//flux for continuity equation//
inline double Fluxcon(double h, double q)
{
	return q;
}

//flux for momentum equation//
inline double Fluxmom(double h, double q)
{
	return q*q/h+g*h*h/2.0;

}

//hll flux//
inline void HLLFlux(double FLR[], double hL, double hR, double qL, double qR)
{
	double hst,ust;

	//estimastion of hst and ust//
	TRRS(hst,ust,hL,hR,qL,qR);
	//TSRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	
	//wave speed estimation//
	double SL=SLeft(hst,hL,qL);
	double SR=SRight(hst,hR,qR);
	
	if(SL>=0)
	{
		FLR[0]=Fluxcon(hL,qL);
		FLR[1]=Fluxmom(hL,qL);
	}
	else if(SR<=0)
	{
		FLR[0]=Fluxcon(hR,qR);
		FLR[1]=Fluxmom(hR,qR);
	}
	else
	{
		FLR[0]=(SR*Fluxcon(hL,qL)-SL*Fluxcon(hR,qR)+SR*SL*(hR-hL))/(SR-SL);
		FLR[1]=(SR*Fluxmom(hL,qL)-SL*Fluxmom(hR,qR)+SR*SL*(qR-qL))/(SR-SL);
	}
}

inline void output(double h[], double z[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="h_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<h[i]+z[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<z[i]<<endl;
	}
	
	count+=1;
}

//flux limiter superbee//
inline double superbee(double d1, double d2, double delta, double omega)
{
	double zeta;

	if(d1*d2<=0)
	{
		zeta=0.0;
	}
	else
	{
		if(d1/d2<=0.5)
		{
			zeta=2.0*d1/d2;
		}
		else if(d1/d2<=1.0)
		{
			zeta=1.0;
		}
		else
		{
			double zetaR=2.0/(1.0-omega+(1.0+omega)*d1/d2);
			zeta=min(zetaR,d1/d2);
			zeta=min(zeta,2.0);
		}
	}
	
	return zeta*delta;
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double h[], double q[], double hiLn[], double hiRn[], double qiLn[], double qiRn[])
{
	double hiL[Node];
	double hiR[Node];
	double qiL[Node];
	double qiR[Node];
	
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dhl=h[i]-h[i-1];
		double dhr=h[i+1]-h[i];
		double dql=q[i]-q[i-1];
		double dqr=q[i+1]-q[i];
		
		//slope//
		double omega=0.0;
		double delh=(1.0+omega)/2.0*dhl+(1.0-omega)/2.0*dhr;
		double delq=(1.0+omega)/2.0*dql+(1.0-omega)/2.0*dqr;
		
		//slope limiter//
		delh=superbee(dhl,dhr,delh,omega);
		delq=superbee(dql,dqr,delq,omega);
		
		//boundary extrapolation//
		hiL[i]=h[i]-0.5*delh;
		hiR[i]=h[i]+0.5*delh;
		qiL[i]=q[i]-0.5*delq;
		qiR[i]=q[i]+0.5*delq;
	
		//time evolution of boundary extrapolated values//
		hiLn[i]=hiL[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		hiRn[i]=hiR[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		qiLn[i]=qiL[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
		qiRn[i]=qiR[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
	}
	
	//BC//
	//i=0//
	hiLn[0]=hiLn[1];
	hiRn[0]=hiRn[1];
	qiLn[0]=qiLn[1];
	qiRn[0]=qiRn[1];
	
	//i=Node-1//
	hiLn[Node-1]=hiLn[Node-2];
	hiRn[Node-1]=hiRn[Node-2];
	qiLn[Node-1]=qiLn[Node-2];
	qiRn[Node-1]=qiRn[Node-2];
}

int main()
{
	const int n=200;//number of cells
	const int Node=n+1;
	double L=1.0;
	double dx=L/double(n);
	double dt=0.0001;
	double TotalTime=0.15;
	int div=20;//for output
	double q[Node];
	double h[Node];
	double qn[Node];
	double hn[Node];
	double FL[2],FR[2];
	double InithL=1.0;
	double InithR=0.1;
	double z[Node];
	double I[Node];
	double mn=0.01;
	//for reconstruction//
	double hiLn[Node];
	double hiRn[Node];
	double qiLn[Node];
	double qiRn[Node];
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithL;
	}
	for(int i=Node/2;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithR;
	}
	
	//bottom//
	for(int i=0;i<Node;i++)
	{
		z[i]=0.0;
		double a=0.1-3.0*(float(i)*dx-0.5)*(float(i)*dx-0.5);
		if(a>0.0) z[i]=a;
		z[i]=0.0;
		//cout<<z[i]<<endl;
	}
	
	//slope//
	for(int i=1;i<Node-1;i++)
	{
		I[i]=-(z[i]-z[i-1])/dx;
	}
	//at boundary// 
	I[0]=-(z[1]-z[0])/dx;
	I[Node-1]=-(z[Node-1]-z[Node-2])/dx;
	
	//IC output//
	output(h,z,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,h,q,hiLn,hiRn,qiLn,qiRn);
		
		//HLL//
		for(int i=1;i<Node-1;i++)
		{
			//left flux, between i-1 and i//i-1R,iL
			HLLFlux(FL,hiRn[i-1],hiLn[i],qiRn[i-1],qiLn[i]);
			
			//right flux, between i and i+1//iR,i+1L
			HLLFlux(FR,hiRn[i],hiLn[i+1],qiRn[i],qiLn[i+1]);
			
			hn[i]=h[i]-dt/dx*(FR[0]-FL[0]);
			qn[i]=q[i]-dt/dx*(FR[1]-FL[1]);//+dt*g*h[i]*(I[i]-mn*mn*q[i]*abs(q[i])/pow(h[i],10.0/3.0));
		}

		//BC//
		//left boundary//
		hn[0]=hn[1];
		qn[0]=qn[1];

		//right boundary//
		hn[Node-1]=hn[Node-2];
		qn[Node-1]=qn[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			q[i]=qn[i];
			h[i]=hn[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(h,z,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}

こちらは一般的なMUSCLに書き直したほうです。両者はほぼ一致します。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <sstream>

using namespace std;

const double g=9.8;

//celerity//
inline double a(double h)
{
	return sqrt(g*h);
}

//function for TRRS//
inline double gk(double h0, double hlr)
{
	return sqrt(g/2.0*(h0+hlr)/(h0*hlr));
}

//Riemann Solver Based on Exact Depth Positivity//
inline void EDPRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=(hL+hR)/2.0-(uR-uL)*(hL+hR)/4.0/(aL+aR);
	ust=(uL+uR)/2.0-(hR-hL)*(aL+aR)/(hL+hR);
}

//Two-Rarefaction Riemann Solver//
inline void TRRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double aL=a(hL);
	double aR=a(hR);
	double uL=qL/hL;
	double uR=qR/hR;
	
	hst=1.0/g*((aL+aR)/2.0+(uL-uR)/4.0)*((aL+aR)/2.0+(uL-uR)/4.0);
	ust=(uL+uR)/2.0+aL-aR;
}

//Two-Shock Riemann Solver//
inline void TSRS(double &hst, double &ust, double hL, double hR, double qL, double qR)
{
	double uL=qL/hL;
	double uR=qR/hR;
	
	TRRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	double hcon=hst;
	hst=(gk(hst,hL)*hL+gk(hst,hR)*hR+uL-uR)/(gk(hst,hL)+gk(hst,hR));
	ust=(uL+uR)/2.0+((hcon-hR)*gk(hcon,hR)-(hcon-hL)*gk(hcon,hL))/2.0;
}

//function for HLL//
inline double qk(double hst, double hlr)
{
	double qk=1.0;
	if(hst>hlr) qk=sqrt((hst+hlr)*hst/(hlr*hlr)/2.0);
	return qk;
}


//left wave estimation//
inline double SLeft(double hst, double hL, double qL)
{
	double uL=qL/hL;
	return uL-a(hL)*qk(hst,hL);
}

//right wave estimation//
inline double SRight(double hst, double hR, double qR)
{
	double uR=qR/hR;
	return uR+a(hR)*qk(hst,hR);
}

//flux for continuity equation//
inline double Fluxcon(double h, double q)
{
	return q;
}

//flux for momentum equation//
inline double Fluxmom(double h, double q)
{
	return q*q/h+g*h*h/2.0;

}

//hll flux//
inline void HLLFlux(double FLR[], double hL, double hR, double qL, double qR)
{
	double hst,ust;

	//estimastion of hst and ust//
	TRRS(hst,ust,hL,hR,qL,qR);
	//TSRS(hst,ust,hL,hR,qL,qR);
	//EDPRS(hst,ust,hL,hR,qL,qR);
	
	//wave speed estimation//
	double SL=SLeft(hst,hL,qL);
	double SR=SRight(hst,hR,qR);
	
	if(SL>=0)
	{
		FLR[0]=Fluxcon(hL,qL);
		FLR[1]=Fluxmom(hL,qL);
	}
	else if(SR<=0)
	{
		FLR[0]=Fluxcon(hR,qR);
		FLR[1]=Fluxmom(hR,qR);
	}
	else
	{
		FLR[0]=(SR*Fluxcon(hL,qL)-SL*Fluxcon(hR,qR)+SR*SL*(hR-hL))/(SR-SL);
		FLR[1]=(SR*Fluxmom(hL,qL)-SL*Fluxmom(hR,qR)+SR*SL*(qR-qL))/(SR-SL);
	}
}

inline void output(double h[], double z[], int Node, double dx)
{
	stringstream ss;
	string name;
	ofstream fo;
	static int count=0;
	
	ss<<count;
	name=ss.str();
	name="h_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<h[i]+z[i]<<endl;
	}
	fo<<endl;
	fo<<endl;
	
	for(int i=0;i<Node;i++)
	{
		fo<<dx*float(i)<<" "<<z[i]<<endl;
	}
	
	count+=1;
}

//flux limiter minmod//
inline double minmod(double d1, double d2)
{
	if(d1*d2<=0)
	{
		return 0.0;
	}
	else if(abs(d1)<abs(d2))
	{
		return d1;
	}
	else
	{
		return d2;
	}
}

//reconstruction//
inline void reconst(int Node, double dt, double dx, double h[], double q[], double hiLn[], double hiRn[], double qiLn[], double qiRn[])
{
	double hiL[Node];
	double hiR[Node];
	double qiL[Node];
	double qiR[Node];
	
	//inner cells//
	for(int i=1;i<Node-1;i++)
	{
		//jump//
		double dhl=h[i]-h[i-1];
		double dhr=h[i+1]-h[i];
		double dql=q[i]-q[i-1];
		double dqr=q[i+1]-q[i];
		
		
		
		//slope limiter//
		double k=0.0;
		double b=(3.0-k)/(1.0-k);
		double dhlLim=minmod(dhr,b*dhl);
		double dhrLim=minmod(dhl,b*dhr);
		double dqlLim=minmod(dqr,b*dql);
		double dqrLim=minmod(dql,b*dqr);
		
		double omega=0.0;
		double delh=(1.0+omega)/2.0*dhlLim+(1.0-omega)/2.0*dhrLim;
		double delq=(1.0+omega)/2.0*dqlLim+(1.0-omega)/2.0*dqrLim;
		
		
		//boundary extrapolation//
		hiL[i]=h[i]-0.5*delh;
		hiR[i]=h[i]+0.5*delh;
		qiL[i]=q[i]-0.5*delq;
		qiR[i]=q[i]+0.5*delq;
	
		//time evolution of boundary extrapolated values//
		hiLn[i]=hiL[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		hiRn[i]=hiR[i]-0.5*dt/dx*(Fluxcon(hiR[i],qiR[i])-Fluxcon(hiL[i],qiL[i]));
		qiLn[i]=qiL[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
		qiRn[i]=qiR[i]-0.5*dt/dx*(Fluxmom(hiR[i],qiR[i])-Fluxmom(hiL[i],qiL[i]));
	}
	
	//BC//
	//i=0//
	hiLn[0]=hiLn[1];
	hiRn[0]=hiRn[1];
	qiLn[0]=qiLn[1];
	qiRn[0]=qiRn[1];
	
	//i=Node-1//
	hiLn[Node-1]=hiLn[Node-2];
	hiRn[Node-1]=hiRn[Node-2];
	qiLn[Node-1]=qiLn[Node-2];
	qiRn[Node-1]=qiRn[Node-2];
}

int main()
{
	const int n=200;//number of cells
	const int Node=n+1;
	double L=1.0;
	double dx=L/double(n);
	double dt=0.0001;
	double TotalTime=0.15;
	int div=20;//for output
	double q[Node];
	double h[Node];
	double qn[Node];
	double hn[Node];
	double FL[2],FR[2];
	double InithL=1.0;
	double InithR=0.1;
	double z[Node];
	double I[Node];
	double mn=0.01;
	//for reconstruction//
	double hiLn[Node];
	double hiRn[Node];
	double qiLn[Node];
	double qiRn[Node];
	
	//IC//
	for(int i=0;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithL;
	}
	for(int i=Node/2;i<Node;i++)
	{
		q[i]=0.0;
		h[i]=InithR;
	}
	
	//bottom//
	for(int i=0;i<Node;i++)
	{
		z[i]=0.0;
		double a=0.1-3.0*(float(i)*dx-0.5)*(float(i)*dx-0.5);
		if(a>0.0) z[i]=a;
		z[i]=0.0;
		//cout<<z[i]<<endl;
	}
	
	//slope//
	for(int i=1;i<Node-1;i++)
	{
		I[i]=-(z[i]-z[i-1])/dx;
	}
	//at boundary// 
	I[0]=-(z[1]-z[0])/dx;
	I[Node-1]=-(z[Node-1]-z[Node-2])/dx;
	
	//IC output//
	output(h,z,Node,dx);
	
	//time step// 
	for(int k=1;double(k)*dt<=TotalTime;k++)
	{	
		//reconstruction//
		reconst(Node,dt,dx,h,q,hiLn,hiRn,qiLn,qiRn);
		
		//HLL//
		for(int i=1;i<Node-1;i++)
		{
			//left flux, between i-1 and i//i-1R,iL
			HLLFlux(FL,hiRn[i-1],hiLn[i],qiRn[i-1],qiLn[i]);
			
			//right flux, between i and i+1//iR,i+1L
			HLLFlux(FR,hiRn[i],hiLn[i+1],qiRn[i],qiLn[i+1]);
			
			hn[i]=h[i]-dt/dx*(FR[0]-FL[0]);
			qn[i]=q[i]-dt/dx*(FR[1]-FL[1]);//+dt*g*h[i]*(I[i]-mn*mn*q[i]*abs(q[i])/pow(h[i],10.0/3.0));
		}

		//BC//
		//left boundary//
		hn[0]=hn[1];
		qn[0]=qn[1];

		//right boundary//
		hn[Node-1]=hn[Node-2];
		qn[Node-1]=qn[Node-2];
		
		//update//
		for(int i=0;i<Node;i++)
		{
			q[i]=qn[i];
			h[i]=hn[i];
		}
		
		//output// 
		if(k%div==0)
		{
			output(h,z,Node,dx);
			cout<<"t="<<double(k)*dt<<endl;
		}
	}
	
	return 0;
}