【差分法】MAC法で中心差分を用いてNavier-Stokes方程式を解きました C++コード付き
MAC法(Marker And Cell method)を用いてNavier-Stokes方程式を数値的に解いてみました。テスト問題としてよく取り上げられる2次元キャビティー流れです。水で満たされた正方形があり、上部の壁だけ右へ一定の速さで動いていきます。最初は静止していた水が、上部の壁に引きずられて動き始めます。そして、最終的には渦が形成されます。水で満たされている領域を考えるので、自由水面を考える必要が無い、閉じた領域で水の出入りが無い、といった特徴があるので、テスト問題としてよく取り上げられています。離散化は以下を見てください。河村哲也著『流体解析の基礎』のpp.65-71も非常に参考になります。

- 作者: 河村哲也
- 出版社/メーカー: 朝倉書店
- 発売日: 2014/03/26
- メディア: 単行本
- この商品を含むブログ (1件) を見る
計算条件ですが、正方形のサイズは1×1、上部の壁は右へ速さ1で移動、節点数は31×31、セル数は30×30、レイノルズ数は100であるとしています。高レイノルズ数の場合は空間解像度を上げ、時間差分間隔を十分に短くとる必要があります。他には、風上差分などを用いて移流項の離散化を工夫したり、乱流モデルを導入する必要があります。今回は単純に中心差分で離散化しています。
とりあえず計算結果です。
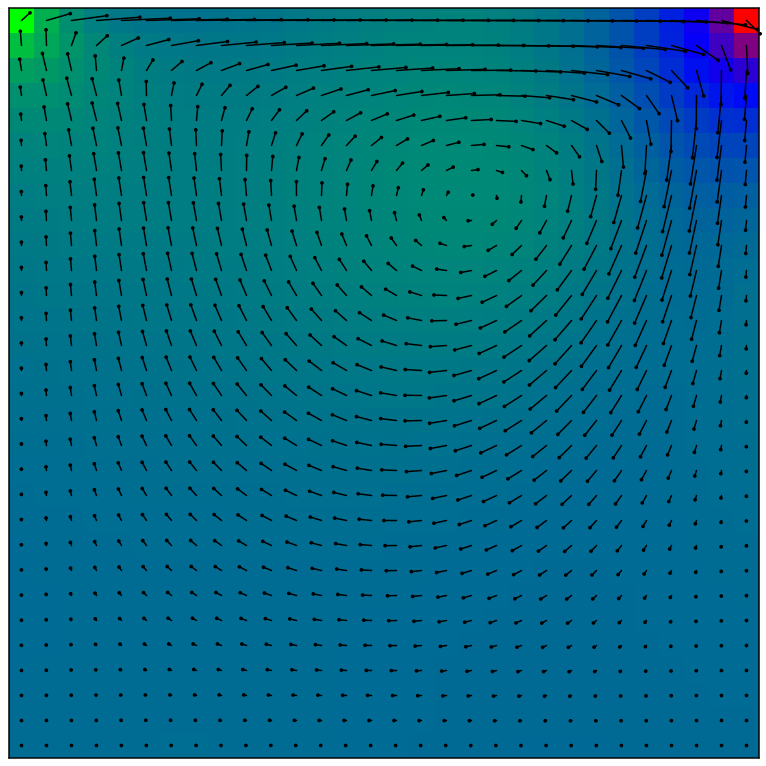
グラデーションが圧力をあらわしています。緑が圧力が小さい、青が中間、赤が圧力が高いことをあらわしています。キャビティーの左上で圧力が小さく、右上で高くなっていることがわかります。これは上部の壁が右へと動いているからです。黒い線は各セルにおける流速ベクトルを示しています。黒い丸が付いている方向へと流れています。黒い丸だけの所は流れが無いと考えて下さい。中心よりちょっと右上を起点とした時計回りの渦が形成されていることがわかります。また、上部ほど流速が大きいことがわかります。
ではコードです。まずは関数を使わず二次元配列で書いたほうです。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; int main() { const int xn=31; const int yn=31; int i,j,k,l; double divv; double err; double udiv,vdiv; double ua,ub,va,vb; double pres; double uad,vad; double udif,vdif; double umid,vmid; double u[xn+2][yn+1],v[xn+1][yn+2],p[xn+1][yn+1];//velocities and pressure double d[xn+1][yn+1];//for continuity double r[xn+1][yn+1];//for r.h.s. of Poisson equation double uwall=1.; double dx=1./(double)(xn-1); double dy=1./(double)(yn-1); double dt=0.001; double re=100; double C1=0.5*dy*dy/(dx*dx+dy*dy); double C2=0.5*dx*dx/(dx*dx+dy*dy); double C3=0.5*dy*dy/(1.+dy*dy/(dx*dx)); int lm=20000; int km=100; ofstream fk,ff; fk.open("vel.txt"); ff.open("pre.txt"); //initialization// for(i=0;i<xn+1;i++) { for(j=0;j<yn+1;j++) { p[i][j]=0.; } } for(i=0;i<xn+2;i++) { for(j=0;j<yn+1;j++) { u[i][j]=0.; } } for(i=0;i<xn+1;i++) { for(j=0;j<yn+2;j++) { v[i][j]=0.; } } //time step// for(l=1;l<=lm;l++) { //BC for left and right// for(j=0;j<yn+1;j++) { u[1][j]=0.; u[0][j]=u[2][j]; v[0][j]=-v[1][j]; u[xn][j]=0.; u[xn+1][j]=u[xn-1][j]; v[xn][j]=-v[xn-1][j]; } v[0][yn+1]=-v[1][yn+1]; v[xn][yn+1]=-v[xn-1][yn+1]; //BC for bottom and top// for(i=0;i<xn+1;i++) { v[i][1]=0.; v[i][0]=v[i][2]; u[i][0]=-u[i][1]; v[i][yn]=0.; v[i][yn+1]=v[i][yn-1]; u[i][yn]=2.0*uwall-u[i][yn-1];//for wall } u[xn+1][0]=-u[xn][0]; u[xn+1][yn]=-u[xn][yn]; divv=0.; //r.h.s. of Poisson equation for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { udiv=(u[i+1][j]-u[i][j])/dx; vdiv=(v[i][j+1]-v[i][j])/dy; d[i][j]=udiv+vdiv; divv+=fabs(udiv+vdiv); ua=(u[i][j]+u[i+1][j]+u[i+1][j+1]+u[i][j+1])/4.0; ub=(u[i][j]+u[i+1][j]+u[i+1][j-1]+u[i][j-1])/4.0; va=(v[i][j]+v[i][j+1]+v[i+1][j+1]+v[i+1][j])/4.0; vb=(v[i][j]+v[i][j+1]+v[i-1][j+1]+v[i-1][j])/4.0; r[i][j]=-udiv*udiv-2.0*(ua-ub)*(va-vb)/dx/dy-vdiv*vdiv+1.0/dt*(udiv+vdiv); } } //Poisson equation// for(k=1;k<=km;k++) { err=0.; //Neumann BC// for(j=0;j<yn+1;j++) { p[0][j]=p[1][j]-1.0/re*2.0*u[2][j]; p[xn][j]=p[xn-1][j]+1.0/re*2.0*u[xn-1][j]; } for(i=0;i<xn+1;i++) { p[i][0]=p[i][1]-1.0/re*2.0*v[i][2]; p[i][yn]=p[i][yn-1]+1.0/re*2.0*v[i][yn-1]; } //iteration SOR// for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { pres=C1*(p[i+1][j]+p[i-1][j])+C2*(p[i][j+1]+p[i][j-1])-C3*r[i][j]-p[i][j]; err+=pres*pres; p[i][j]=pres+p[i][j]; } } if(err<=0.000005) break; } if(l%1000==0) cout<<l<<" "<<err<<" "<<divv<<endl; //u// for(i=2;i<xn;i++) { for(j=1;j<yn;j++) { vmid=(v[i][j]+v[i][j+1]+v[i-1][j+1]+v[i-1][j])/4.0; uad=u[i][j]*(u[i+1][j]-u[i-1][j])/2.0/dx+vmid*(u[i][j+1]-u[i][j-1])/2.0/dy; udif=(u[i+1][j]-2.0*u[i][j]+u[i-1][j])/dx/dx+(u[i][j+1]-2.0*u[i][j]+u[i][j-1])/dy/dy; u[i][j]=u[i][j]+dt*(-uad-(p[i][j]-p[i-1][j])/dx+1.0/re*udif); } } //v// for(i=1;i<xn;i++) { for(j=2;j<yn;j++) { umid=(u[i][j]+u[i+1][j]+u[i+1][j-1]+u[i][j-1])/4.0; vad=umid*(v[i+1][j]-v[i-1][j])/2.0/dx+v[i][j]*(v[i][j+1]-v[i][j-1])/2.0/dy; vdif=(v[i+1][j]-2.0*v[i][j]+v[i-1][j])/dx/dx+(v[i][j+1]-2.0*v[i][j]+v[i][j-1])/dy/dy; v[i][j]=v[i][j]+dt*(-vad-(p[i][j]-p[i][j-1])/dy+1.0/re*vdif); } } } for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { fk<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<(u[i][j]+u[i+1][j])/2.0<<" "<<(v[i][j]+v[i][j+1])/2.0<<endl; ff<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<p[i][j]<<endl; } } return 0; }
次に、関数を使って整理し一次元配列で書いたほうです。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; inline void rhspoi(int xn, int yn, double u[], double v[], double &uwall, double &divv, double r[], double &dx, double &dy, double &dt) { int i,j; double udiv,vdiv; double ua,ub,va,vb; //BC for left and right// for(j=0;j<yn+1;j++) { u[1*(yn+1)+j]=0.; u[0*(yn+1)+j]=u[2*(yn+1)+j]; v[0*(yn+2)+j]=-v[1*(yn+2)+j]; u[xn*(yn+1)+j]=0.; u[(xn+1)*(yn+1)+j]=u[(xn-1)*(yn+1)+j]; v[xn*(yn+2)+j]=-v[(xn-1)*(yn+2)+j]; } v[0*(yn+2)+yn+1]=-v[1*(yn+2)+yn+1]; v[xn*(yn+2)+yn+1]=-v[(xn-1)*(yn+2)+yn+1]; //BC for bottom and top// for(i=0;i<xn+1;i++) { v[i*(yn+2)+1]=0.; v[i*(yn+2)+0]=v[i*(yn+2)+2]; u[i*(yn+1)+0]=-u[i*(yn+1)+1]; v[i*(yn+2)+yn]=0.; v[i*(yn+2)+yn+1]=v[i*(yn+2)+yn-1]; u[i*(yn+1)+yn]=2.0*uwall-u[i*(yn+1)+yn-1];//for wall } u[(xn+1)*(yn+1)+0]=-u[xn*(yn+1)+0]; u[(xn+1)*(yn+1)+yn]=-u[xn*(yn+1)+yn]; divv=0.; //r.h.s. of Poisson equation for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { udiv=(u[(i+1)*(yn+1)+j]-u[i*(yn+1)+j])/dx; vdiv=(v[i*(yn+2)+j+1]-v[i*(yn+2)+j])/dy; divv+=fabs(udiv+vdiv); ua=(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j]+u[(i+1)*(yn+1)+j+1]+u[i*(yn+1)+j+1])/4.0; ub=(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j]+u[(i+1)*(yn+1)+j-1]+u[i*(yn+1)+j-1])/4.0; va=(v[i*(yn+2)+j]+v[i*(yn+2)+j+1]+v[(i+1)*(yn+2)+j+1]+v[(i+1)*(yn+2)+j])/4.0; vb=(v[i*(yn+2)+j]+v[i*(yn+2)+j+1]+v[(i-1)*(yn+2)+j+1]+v[(i-1)*(yn+2)+j])/4.0; r[i*(yn+1)+j]=-udiv*udiv-2.0*(ua-ub)*(va-vb)/dx/dy-vdiv*vdiv+1.0/dt*(udiv+vdiv); } } } inline void poi(int &km, int xn, int yn, double p[], double &dx, double &dy, double r[], double &err, double &re, double u[], double v[]) { int i,j,k; double C1=0.5*dy*dy/(dx*dx+dy*dy); double C2=0.5*dx*dx/(dx*dx+dy*dy); double C3=0.5*dy*dy/(1.+dy*dy/(dx*dx)); double pres; //Poisson equation// for(k=1;k<=km;k++) { err=0.; //Neumann BC// for(j=0;j<yn+1;j++) { p[0*(yn+1)+j]=p[1*(yn+1)+j]-1.0/re*2.0*u[2*(yn+1)+j]; p[xn*(yn+1)+j]=p[(xn-1)*(yn+1)+j]+1.0/re*2.0*u[(xn-1)*(yn+1)+j]; } for(i=0;i<xn+1;i++) { p[i*(yn+1)+0]=p[i*(yn+1)+1]-1.0/re*2.0*v[i*(yn+2)+2]; p[i*(yn+1)+yn]=p[i*(yn+1)+yn-1]+1.0/re*2.0*v[i*(yn+2)+yn-1]; } //iteration// for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { pres=C1*(p[(i+1)*(yn+1)+j]+p[(i-1)*(yn+1)+j])+C2*(p[i*(yn+1)+j+1]+p[i*(yn+1)+j-1])-C3*r[i*(yn+1)+j]-p[i*(yn+1)+j]; err+=pres*pres; p[i*(yn+1)+j]=pres+p[i*(yn+1)+j]; } } if(err<=0.000005) break; } } inline void vel(int xn, int yn, double u[], double v[], double &dx, double &dy, double &dt, double p[], double &re) { int i,j; double uad,vad; double udif,vdif; double umid,vmid; //u// for(i=2;i<xn;i++) { for(j=1;j<yn;j++) { vmid=(v[i*(yn+2)+j]+v[i*(yn+2)+j+1]+v[(i-1)*(yn+2)+j+1]+v[(i-1)*(yn+2)+j])/4.0; uad=u[i*(yn+1)+j]*(u[(i+1)*(yn+1)+j]-u[(i-1)*(yn+1)+j])/2.0/dx+vmid*(u[i*(yn+1)+j+1]-u[i*(yn+1)+j-1])/2.0/dy; udif=(u[(i+1)*(yn+1)+j]-2.0*u[i*(yn+1)+j]+u[(i-1)*(yn+1)+j])/dx/dx+(u[i*(yn+1)+j+1]-2.0*u[i*(yn+1)+j]+u[i*(yn+1)+j-1])/dy/dy; u[i*(yn+1)+j]=u[i*(yn+1)+j]+dt*(-uad-(p[i*(yn+1)+j]-p[(i-1)*(yn+1)+j])/dx+1.0/re*udif); } } //v// for(i=1;i<xn;i++) { for(j=2;j<yn;j++) { umid=(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j]+u[(i+1)*(yn+1)+j-1]+u[i*(yn+1)+j-1])/4.0; vad=umid*(v[(i+1)*(yn+2)+j]-v[(i-1)*(yn+2)+j])/2.0/dx+v[i*(yn+2)+j]*(v[i*(yn+2)+j+1]-v[i*(yn+2)+j-1])/2.0/dy; vdif=(v[(i+1)*(yn+2)+j]-2.0*v[i*(yn+2)+j]+v[(i-1)*(yn+2)+j])/dx/dx+(v[i*(yn+2)+j+1]-2.0*v[i*(yn+2)+j]+v[i*(yn+2)+j-1])/dy/dy; v[i*(yn+2)+j]=v[i*(yn+2)+j]+dt*(-vad-(p[i*(yn+1)+j]-p[i*(yn+1)+j-1])/dy+1.0/re*vdif); } } } int main() { const int xn=31; const int yn=31; int i,j,l; double divv; double err; double *u=new double[(xn+2)*(yn+1)]; double *v=new double[(xn+1)*(yn+2)]; double *p=new double[(xn+1)*(yn+1)]; double *r=new double[(xn+1)*(yn+1)];//for r.h.s. of Poisson equation double uwall=1.; double dx=1./(double)(xn-1); double dy=1./(double)(yn-1); double dt=0.001; double re=100; int lm=20000; int km=100; ofstream fk,ff; fk.open("vel.txt"); ff.open("pre.txt"); //initialization// for(i=0;i<xn+1;i++) { for(j=0;j<yn+1;j++) { p[i*(yn+1)+j]=0.; } } for(i=0;i<xn+2;i++) { for(j=0;j<yn+1;j++) { u[i*(yn+1)+j]=0.; } } for(i=0;i<xn+1;i++) { for(j=0;j<yn+2;j++) { v[i*(yn+2)+j]=0.; } } //time step// for(l=1;l<=lm;l++) { rhspoi(xn,yn,u,v,uwall,divv,r,dx,dy,dt); poi(km,xn,yn,p,dx,dy,r,err,re,u,v); if(l%1000==0) cout<<l<<" "<<err<<" "<<divv<<endl; vel(xn,yn,u,v,dx,dy,dt,p,re); } //output for(i=1;i<xn;i++) { for(j=1;j<yn;j++) { fk<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<(u[i*(yn+1)+j]+u[(i+1)*(yn+1)+j])/2.0<<" "<<(v[i*(yn+2)+j]+v[i*(yn+2)+j+1])/2.0<<endl; ff<<double((i-0.5)*dx)<<" "<<double((j-0.5)*dy)<<" "<<p[i*(yn+1)+j]<<endl; } } delete[] u,v,p,r; return 0; }
今までNavier-Stokes方程式の数値計算に挑戦してみたいろ思っていましたが、なんだか難しそうなので敬遠していました。しかし、いざやってみると実際にやっていることはPoisson方程式をGauss-Seidel法で解くことで、精々200行程度で書けることがわかりました。自分でやってみるのはとても大事ですね。
今後は温度も考慮して山越え気流の解析をやってみたいですね。
MAC+風上差分