【有限体積法】1次元移流方程式を流束制限関数(superbee)で解く C++コード付き
今回は1次元移流方程式を有限体積法(流束制限関数)で解いていきます。C++コード付きです。
1次元移流方程式とは
のような一階の偏微分方程式のことをいいます。ここで、 は溶質の濃度、
は風などによる移流速度です。
さて、slope limiterというのは、補間した変数自体(この場合 )を単調性を保つように制限するものということができます。ここで制限を行う関数をflux limiter function(流束制限関数)といいます。flux limiter functionには様々な種類があるのですが、今回はsuperbee関数を用いています。詳しくは別記事で説明します。お待ちください。
境界条件は2パターンあります。すなわち、
Case 1, でDirichlet条件を課す
(の値を指定)
Case 2, でDirichlet条件を課す
( の値を指定)
です。それぞれコード上ではbc=1、bc=2に対応しています。特性曲線の向きを考えるとわかるのですが、 でDirichlet条件を課すのは移流速度が正の場合です。直観的には波が境界の外から内部へ入って来る様子を表しています。なので、
では境界条件は必要ありません。これが移流方程式の境界条件の独特な部分です。逆に移流速度が負の場合は
でDirichlet条件を課します。
今回の計算条件は、移流速度が負 で、分割数は400、時間刻みは0.001、領域の広さは
、初期条件は領域の右端の矩形波(長方形の波)です。
コードです。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <string> #include <sstream> using namespace std; inline double limiter(double d1, double d2)//superbee { if(d1*d2<=0) { return 0.0; } else if(d1/d2<=0.5) { return 2.0*d1/d2; } else if(d1/d2<=1) { return 1.0; } else if(d1/d2<=2) { return d1/d2; } else { return 2.0; } } inline void solve(double x[], int &Node, double &dt, double &dx, double &V) { int i; for(i=2;i<Node-2;i++) { x[i]=x[i]-dt/dx*(max(V,0.0)*(x[i]+0.5*limiter(x[i]-x[i-1],x[i+1]-x[i])*(x[i+1]-x[i]) -(x[i-1]+0.5*limiter(x[i-1]-x[i-2],x[i]-x[i-1])*(x[i]-x[i-1]))) -max(-V,0.0)*(x[i+1]+0.5*limiter(x[i+2]-x[i+1],x[i+1]-x[i])*(x[i]-x[i+1]) -(x[i]+0.5*limiter(x[i+1]-x[i],x[i]-x[i-1])*(x[i-1]-x[i])))); } } inline void boundary(int &bc, double &D0, double x[], double &V, int &Node, double &dt, double &dx) { double xo; int i; if(bc==1) { x[0]=D0; xo=2.0*x[0]-x[1]; i=1; x[i]=x[i]-dt/dx*V*(x[i]+0.5*limiter(x[i]-x[i-1],x[i+1]-x[i])*(x[i+1]-x[i]) -(x[i-1]+0.5*limiter(x[i-1]-xo,x[i]-x[i-1])*(x[i]-x[i-1]))); i=Node-1; x[i]=x[i]-dt/dx*V*(x[i]+0.5*limiter(x[i]-x[i-1],x[i+1]-x[i])*(x[i+1]-x[i]) -(x[i-1]+0.5*limiter(x[i-1]-x[i-2],x[i]-x[i-1])*(x[i]-x[i-1]))); } if(bc==2) { x[Node-1]=D0; xo=2.0*x[0]-x[1]; i=Node-2; x[i]=x[i]-dt/dx*V*(x[i+1]+0.5*limiter(xo-x[i+1],x[i+1]-x[i])*(x[i]-x[i+1]) -(x[i]+0.5*limiter(x[i+1]-x[i],x[i]-x[i-1])*(x[i-1]-x[i]))); i=0; x[i]=x[i]-dt/dx*V*(x[i+1]+0.5*limiter(x[i+2]-x[i+1],x[i+1]-x[i])*(x[i]-x[i+1]) -(x[i]+0.5*limiter(x[i+1]-x[i],x[i]-x[i-1])*(x[i-1]-x[i]))); } } inline void text(int &i,double x[], double &dx, int &Node) { int j; stringstream ss; string name; ofstream fo; ss<<i; name=ss.str(); name="Answer_" + name + ".txt"; fo.open(name.c_str ()); for(j=0;j<Node;j++) { fo<<dx*float(j)<<" "<<x[j]<<endl; } } int main() { int i; int Partition=400; int Node=Partition+1; double LL=1.0; double dx=LL/(Node-1); double dt=0.001; double NT=7500; double eps=pow(2.0,-50); double V=-0.1; int bc=2;//bc=1 left Dirichlet (V>=0), bc=2 right Dirichlet (V<0) double D0=0.0;//for Dirichlet double *x=new double[Node]; ofstream fk; fk.open("Answer_0.txt"); //initial condition// for(i=0;i<Node;i++) { x[i]=0.0; //if((i>=40)&&(i<=80)) x[i]=1.0; if((i>=320)&&(i<=360)) x[i]=1.0; fk<<dx*float(i)<<" "<<x[i]<<endl; } for(i=1;i<=NT;i++) { solve(x,Node,dt,dx,V); boundary(bc,D0,x,V,Node,dt,dx); if(i%1500==0) { cout<<i<<endl; text(i,x,dx,Node); } } delete[] x; return 0; }
計算結果を見てみましょう。
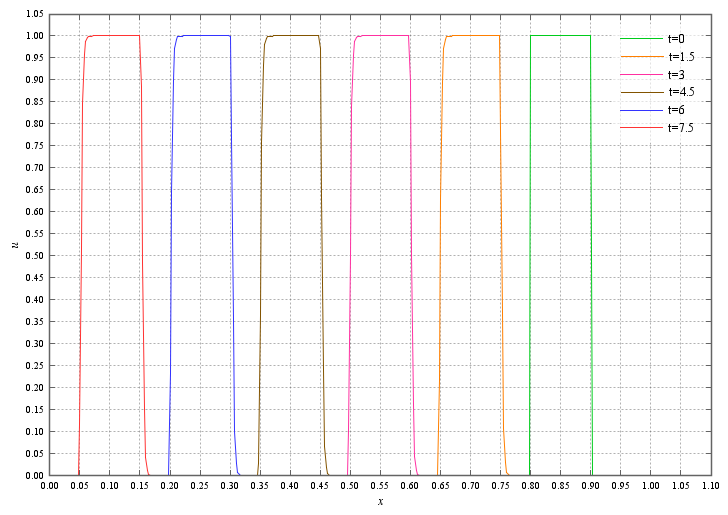
初期条件である右端の矩形波が時間がすすむにつれて左へと流されていきます。minmod関数よりもシャープなプロファイルを得られています。ただし、superbeeはminmodよりも不安定であると言われています。
離散化の詳細は後でまとめます。