【有限体積法】1次元定常移流拡散方程式をハイブリッド法で解く C++コード付き
今回は1次元定常移流拡散方程式を有限体積法(ハイブリッド法)で解いていきます。C++コード付きです。
1次元定常移流拡散方程式とは
のような二階の常微分方程式のことをいいます。ここで、 は溶質の濃度、
は風などによる移流速度、
は拡散の効果を表す拡散係数と解釈することができます。ある溶質が移流や拡散のもとでどのような分布をとるか求めるのがこの問題です。
前回は中心差分で解きましたが、移流が卓越する場合中心差分は不安定になるので対策が必要です。
今回はハイブリッド法を用います。ハイブリッド法とは簡単に言うと、移流が大きくない場合は中心差分を使い、移流が大きい場合は風上差分を使う方法のことです。境界条件は前回と同じく3パターン用意しました。すなわち、
Case 1, と
でDirichlet条件を課す
( と
の値を指定)
Case 2, でNeumann条件、
でDirichlet条件を課す
( と
の値を指定)
Case 3, でDirichlet条件、
でNeumann条件を課す
( と
の値を指定)
です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。
コードです。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> #include <algorithm> using namespace std; //Gauss-Seidel// inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps) { int i,k; double in,sum,max; for(k=0;k<100000;k++) { max=0.0; in=x[0]; for(i=0;i<Node;i++) { in=x[i]; x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i]; if(max<abs(in-x[i])) max=abs(in-x[i]); } if(eps>max) break; } } //TDMA//a:diagonal,c:left,b:right, inline void tdma(double a[], double c[], double b[], double d[], double x[], int size) { int i; double *P=new double[size]; double *Q=new double[size]; //first step// P[0]=-b[0]/a[0]; Q[0]=d[0]/a[0]; //second step// for(i=1;i<size;i++) { P[i]=-b[i]/(a[i]+c[i]*P[i-1]); Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]); } //third step, backward// x[size-1]=Q[size-1]; for(i=size-2;i>-1;i=i-1) { x[i]=P[i]*x[i+1]+Q[i]; } delete [] P,Q; } inline void mat(double D[],double L[],double R[],double b[],double f[], int &Node, double &dx, double &V, double &Diff) { int i; for(i=1;i<Node;i++) { //Diffusion// L[i]=-max(V,max(Diff/dx+V/2.0,0.0)); D[i]=max(V,max(Diff/dx+V/2.0,0.0))+max(-V,max(Diff/dx-V/2.0,0.0)); R[i]=-max(-V,max(Diff/dx-V/2.0,0.0)); //Source// b[i]=-f[i]*dx; } } inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node, double &dx, double f[], double &V, double &Diff) { if(bc==1) { D[0]=1.0;R[0]=0.0;b[0]=D0; L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1; } if(bc==2) { L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1; D[0]=max(V,max(Diff/dx+V/2.0,0.0))-V; R[0]=-max(-V,max(Diff/dx-V/2.0,0.0)); b[0]=-f[0]*dx/2.0-N0*Diff; } if(bc==3) { D[0]=1.0;R[0]=0.0;b[0]=D0; L[Node-1]=-max(V,max(Diff/dx+V/2.0,0.0)); D[Node-1]=max(-V,max(Diff/dx-V/2.0,0.0))+V; b[Node-1]=-f[Node-1]*dx/2.0+N1*Diff; } } int main() { int i; int Partition=100; int Node=Partition+1;//the number of cells is equal to the number of nodes double LL=1.0; double dx=LL/(Node-1); double eps=pow(2.0,-50); int bc=1;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann double D0=0.0; double D1=1.0; double N0=5.0; double N1=3.0; double Diff=0.01; double V=0.1; double *b = new double[Node]; double *x = new double[Node]; double *f = new double[Node]; double *D = new double[Node]; double *L = new double[Node]; double *R = new double[Node]; for(i=0;i<Node;i++) { b[i]=0.0;x[i]=0.0;f[i]=0.0;D[i]=0.0;L[i]=0.0;R[i]=0.0; } ofstream fk; fk.open("answer.txt"); mat(D,L,R,b,f,Node,dx,V,Diff); boundary(bc,D0,D1,N0,N1,D,L,R,b,Node,dx,f,V,Diff); //Gauss-Seidel or TDMA// //GS(D,L,R,x,b,Node,eps); tdma(D,L,R,b,x,Node); for(i=0;i<Node;i++) cout<<x[i]<<endl; for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl; delete[] b,x,f,D,L,R; return 0; }
計算結果を見てみましょう。
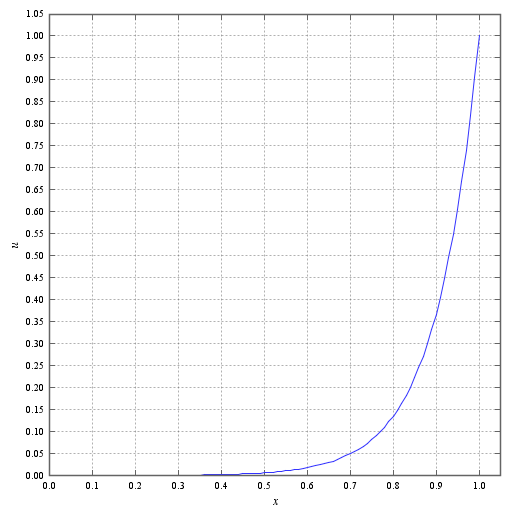
中心差分の場合の結果と似ていますが、それはセル数が十分にあるからです。今後セル数が少ない場合の他の手法との比較をしたいと思います。