【有限体積法】1次元Poisson方程式(ポアソン方程式)を有限体積法で解く C++コード付き
有限体積法のほうもぼちぼち1次元の場合から解説していきます!
今回は有限体積法の勉強で最初に解くであろう、1次元Poisson方程式を有限要素法(Galerkin法)で解くC++コードを公開します。
普通の有限体積法で離散化します。二次元配列は一次元配列に収納しています。二次元配列を使ったほうが行列を足し合わせるときにわかりやすいので、初心者の方はそれでよいと思います。ただ要素数が増えてくると、二次元配列は重いので一次元配列のみで処理するのがおすすめです。
Poisson方程式とは
のような二階の偏微分方程式のことを言います。ここで は既知の関数です。1次元の場合は
となります。以下では とします。このとき解析解を求めることができます。
境界条件は3パターン扱うことができるようにつくってあります。すなわち、
Case 1, と
でDirichlet条件を課す
( と
の値を指定)
Case 2, でNeumann条件、
でDirichlet条件を課す
( と
の値を指定)
Case 3, でDirichlet条件、
でNeumann条件を課す
( と
の値を指定)
です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。
コードです。今回は行列が三重対角行列になるので、配列のDに対角要素を、Lに対角要素の左隣の要素を、Rに対角要素の右隣の要素を格納しています。
#include <iostream> #include <cmath> #include <fstream> #include <iomanip> using namespace std; //Gauss-Seidel// inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps) { int i,k; double in,sum,max; for(k=0;k<100000;k++) { max=0.0; in=x[0]; for(i=0;i<Node;i++) { in=x[i]; x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i]; if(max<abs(in-x[i])) max=abs(in-x[i]); } if(eps>max) break; } } //TDMA//a:diagonal,c:left,b:right, inline void tdma(double a[], double c[], double b[], double d[], double x[], int size) { int i; double *P=new double[size]; double *Q=new double[size]; //first step// P[0]=-b[0]/a[0]; Q[0]=d[0]/a[0]; //second step// for(i=1;i<size;i++) { P[i]=-b[i]/(a[i]+c[i]*P[i-1]); Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]); } //third step, backward// x[size-1]=Q[size-1]; for(i=size-2;i>-1;i=i-1) { x[i]=P[i]*x[i+1]+Q[i]; } delete [] P,Q; } inline void mat(double D[],double L[],double R[],double b[],double f[], int &Node, double &dx) { int i; for(i=1;i<Node;i++) { L[i]=1.0/dx; D[i]=-2.0/dx; R[i]=1.0/dx; b[i]=-f[i]*dx; } } inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node, double &dx, double f[]) { if(bc==1) { D[0]=1.0;R[0]=0.0;b[0]=D0; L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1; } if(bc==2) { L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1; D[0]=-1.0/dx;R[0]=1.0/dx;b[0]=-f[0]*dx/2.0+N0; } if(bc==3) { D[0]=1.0;R[0]=0.0;b[0]=D0; L[Node-1]=1.0/dx;D[Node-1]=-1.0/dx;b[Node-1]=-f[Node-1]*dx/2.0-N1; } } int main() { int i; int Partition=100; int Node=Partition+1;//the number of cells is equal to the number of nodes double LL=1.0; double dx=LL/(Node-1); double eps=pow(2.0,-50); int bc=3;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann double D0=1.0; double D1=2.0; double N0=0.0; double N1=0.0; double *b = new double[Node]; double *x = new double[Node]; double *f = new double[Node]; double *D = new double[Node]; double *L = new double[Node]; double *R = new double[Node]; for(i=0;i<Node;i++) { b[i]=0.0;x[i]=0.0;f[i]=1.0;D[i]=0.0;L[i]=0.0;R[i]=0.0; } ofstream fk; fk.open("answer.txt"); mat(D,L,R,b,f,Node,dx); boundary(bc,D0,D1,N0,N1,D,L,R,b,Node,dx,f); //Gauss-Seidel or TDMA// //GS(D,L,R,x,b,Node,eps); tdma(D,L,R,b,x,Node); for(i=0;i<Node;i++) cout<<x[i]<<endl; for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl; delete[] b,x,f,D,L,R; return 0; }
コードの流れですが、まず要素の分割数と境界条件の型(bcの値による)を決め、境界条件の設定(値をどうするか)を行い、関数 mat により行列を作成、関数 boundary で境界条件を行列に反映させ、関数 GS(Gauss-Seidel法)またはTDMAで作成した行列を解き、出力しています。出力はテキストファイル "answer.txt" に出てきます。左の行が 座標で右の行が求めている関数値
です。
それでは計算結果を見てみましょう。
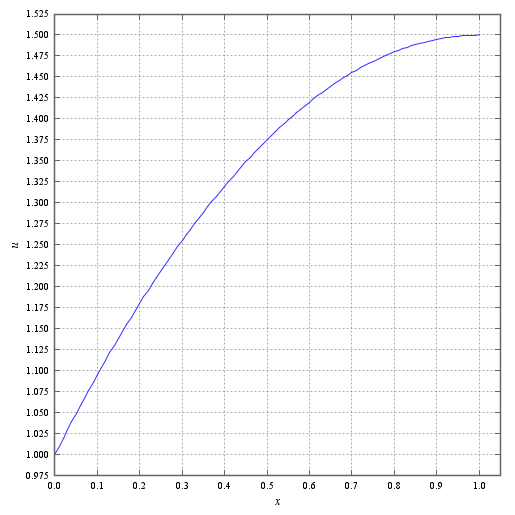
きちんと境界条件が反映されているのがわかるでしょうか。左がDirichlet条件で値は1、右がNeumann条件で値は0です。
今回はコードがメインで離散化の詳細を示していませんが、必ず書くのでお待ちください。
気付いた方がいると思いますが、1次元の場合ほとんどGalerkin法のコードと同じです。主な違いはNeumann境界条件の部分と、行列を組み立てる際に要素ごとではなく、セルごとに行う点です。