【有限要素法】1次元非定常拡散方程式をGalerkin法で解く　C++コード付き

今回は1次元非定常拡散方程式を有限要素法（Galerkin法）で解いていきます。C++コード付きです。1次元非定常拡散方程式は、前に書いた記事「有限要素法のプログラミングを勉強するときにどの順序で学ぶのがよいか？」で紹介した、有限要素法を学ぶ場合に三番目に解くべき方程式です。

1次元非定常拡散方程式とは

$\displaystyle \frac{\partial u}{\partial t}=D\frac{\partial^2 u}{\partial x^2}, \quad x \in [0, L]$

のような偏微分方程式のことをいいます。ここで、 $u(t,x)$ は熱や溶質の濃度、 $D$ は拡散の効果を表す拡散係数と解釈することができます。熱またはある溶質が時間が経過するにつれてどのような分布をとるか（拡散していくか）求めるのがこの問題です。 $u$ は時間方向と空間方向ともに変化するので二変数関数 $u(t,x)$ となっています。前に説明した1次元Poisson方程式を時間発展させたものにあたります。境界条件は前回と同じく3パターン用意しました。すなわち、

Case 1, $x=0$ と $x=L$ でDirichlet条件を課す
（ $u(t,0)$ と $u(t,L)$ の値を指定）
Case 2, $x=0$ でNeumann条件、 $x=L$ でDirichlet条件を課す
（ $\frac{ \partial u }{ \partial x }(t,0)$ と $u(t,L)$ の値を指定）
Case 3, $x=0$ でDirichlet条件、 $x=L$ でNeumann条件を課す
（ $u(t,0)$ と $\frac{ \partial u }{ \partial x }(t,L)$ の値を指定）

です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。

空間方向の離散化はGalerkin法、時間方向は $\theta$ 法で離散化しており、今回は $\theta=0.5$ のCrank-Nicolson法を用いています。ちなみに、 $\theta=0$ のとき前進Euler法（陽解法、explicit scheme）に、 $\theta=1$ のときに後退Euler法（完全陰解法、implicit scheme）になります。これらについても今後まとめる予定です。

計算条件については以下のように設定しています。まず、拡散方程式を解く領域は $x\in[0,1$ ]、要素数は100、節点数は101で等分割（ $\Delta x=1/100$ ）、時間刻みは $\Delta t=0.001$ 、計算終了時刻は $t=10$ 、拡散係数は $D=0.01$ 、 $\theta=0.5$ 、境界条件はbc=1（両側Dirichlet条件）で $u(t,0)=0$ と $u(t,1)=0$ 、初期条件は頂点の値が0.5の三角形（下の図参照）です。式で書くと $f(x)=\min(x,1-x)$ です。初期時刻に三角形のような熱の分布を与え、棒の両側をずっと0℃で冷やしたときに、棒の熱はある時間位どのような分布をとるか、という問題です。答えは"Answer_****.txt"（****にはステップ数が入る）に出力されます。1000ステップごとに値が出力されます。一行目が $x$ 座標、二行目がその時刻における $u$ の分布となっています。

コードです。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>
#include <string>
#include <sstream>

using namespace std;

inline void GS(double AD[],double AL[],double AR[],double x[],double xx[],double b[], int &Node, double &eps)
{
	int i,k;
	double in,max;
	
	for(k=0;k<100000;k++)
	{
		max=0.0;
		for(i=0;i<Node;i++)
		{
			in=xx[i];
			xx[i]=(b[i]-(AL[i]*xx[i-1]+AR[i]*xx[i+1]))/AD[i];
			if(max<abs(in-xx[i])) max=abs(in-xx[i]);
		}
		
		if(eps>max) break;
	}
}

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double AD[],double AL[],double AR[],double BD[],double BL[],double BR[],double b[],double f[], int &Ele, double &dx, double &Diff, double &dt, double &theta, int &Node)
{
	int i;
	
	//initialization//
	for(i=0;i<Node;i++)
	{
		AD[i]=0.0;AL[i]=0.0;AR[i]=0.0;BD[i]=0.0;BL[i]=0.0;BR[i]=0.0;
	}
	
	for(i=0;i<Ele;i++)
	{
		//A//
		//teporal//
		AD[i]+=dx*2.0/6.0/dt;
		AR[i]+=dx*1.0/6.0/dt;
		AL[i+1]+=dx*1.0/6.0/dt;
		AD[i+1]+=dx*2.0/6.0/dt;
		
		//diffusion//
		AD[i]+=theta*Diff/dx;
		AR[i]+=theta*-Diff/dx;
		AL[i+1]+=theta*-Diff/dx;
		AD[i+1]+=theta*Diff/dx;
		
		//B//
		//temporal//
		BD[i]+=dx*2.0/6.0/dt;
		BR[i]+=dx*1.0/6.0/dt;
		BL[i+1]+=dx*1.0/6.0/dt;
		BD[i+1]+=dx*2.0/6.0/dt;
		
		//diffusion//
		BD[i]+=-(1.0-theta)*Diff/dx;
		BR[i]+=-(1.0-theta)*-Diff/dx;
		BL[i+1]+=-(1.0-theta)*-Diff/dx;
		BD[i+1]+=-(1.0-theta)*Diff/dx;
	}
}

inline void boundary(int &bc,double AD[],double AL[],double AR[],double BD[],double BL[],double BR[],double b[],int &Node)
{
	if(bc==1)
	{
		AD[0]=1.0;AR[0]=0.0;BD[0]=1.0;BR[0]=0.0;
		AL[Node-1]=0.0;AD[Node-1]=1.0;BL[Node-1]=0.0;BD[Node-1]=1.0;
	}
	if(bc==2)
	{
		AL[Node-1]=0.0;AD[Node-1]=1.0;BL[Node-1]=0.0;BD[Node-1]=1.0;
	}
	if(bc==3)
	{
		AD[0]=1.0;AR[0]=0.0;BD[0]=1.0;BR[0]=0.0;
	}
}

inline void text(int &i,double x[], double &dx, int &Node)
{
	int j;
	
	stringstream ss;
	string name;
	ofstream fo;
	
	ss<<i;
	name=ss.str();
	name="Answer_" + name + ".txt";
	fo.open(name.c_str ());
	
	for(j=0;j<Node;j++)
	{
		fo<<dx*float(j)<<" "<<x[j]<<endl;
	}
}

int main()
{
	int i,j;
	int Ele=100;
	int Node=Ele+1;
	double LL=1.0;
	double dx=LL/Ele;
	double dt=0.001;
	double NT=10000;
	double eps=pow(2.0,-50);
	double Diff=0.01;
	double theta=0.5;
	int bc=1;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=0.0;
	double D1=0.0;
	double N0=0.0;
	double N1=0.0;
	
	double *b=new double[Node];
	double *x=new double[Node];
	double *xx=new double[Node];
	double *f=new double[Node];
	double *AD=new double[Node];
	double *AL=new double[Node];
	double *AR=new double[Node];
	double *BD=new double[Node];
	double *BL=new double[Node];
	double *BR=new double[Node];
	
	ofstream fk;
	fk.open("Answer_0.txt");
	
	//initial condition//
	for(i=0;i<Node;i++)
	{
		x[i]=min(dx*float(i),1.0-dx*float(i));
		fk<<dx*float(i)<<" "<<x[i]<<endl;
	}
	
	mat(AD,AL,AR,BD,BL,BR,b,f,Ele,dx,Diff,dt,theta,Node);
	boundary(bc,AD,AL,AR,BD,BL,BR,b,Node);
	
	for(i=1;i<=NT;i++)
	{
		//for b//
		if(bc==1)
		{
			b[0]=D0;
			b[Node-1]=D1;
		}
		if(bc==2)
		{
			b[Node-1]=D1;
			b[0]=BD[0]*x[0]+BR[0]*x[1]-N0*Diff;
		}
		if(bc==3)
		{
			b[0]=D0;
			b[Node-1]=BL[Node-1]*x[Node-2]+BD[Node-1]*x[Node-1]+N1*Diff;
		}
		
		for(j=1;j<Node-1;j++)
		{
			b[j]=BL[j]*x[j-1]+BD[j]*x[j]+BR[j]*x[j+1];
		}

		//GS or TDMA//
		GS(AD,AL,AR,x,xx,b,Node,eps);
		//tdma(AD,AL,AR,b,xx,Node);
		for(j=0;j<Node;j++) x[j]=xx[j];
		
		if(i%1000==0)
		{
			cout<<i<<endl;
			text(i,x,dx,Node);
		}
	}
	
	delete[] b,x,xx,f,AD,AL,AR,BD,BL,BR;
	
	return 0;
}

以下が計算結果の図です。初期に与えた三角形の熱の分布が時間が経過するにつれてどんどんなまっていく様子が観察できます。両端を冷やしているので棒がどんどん冷めていくのです。もっと時間進行させると領域全体で熱の分布が0に収束していくのが観察できます。

f:id:mutsumunemitsutan:20181022213936p:plain:w500

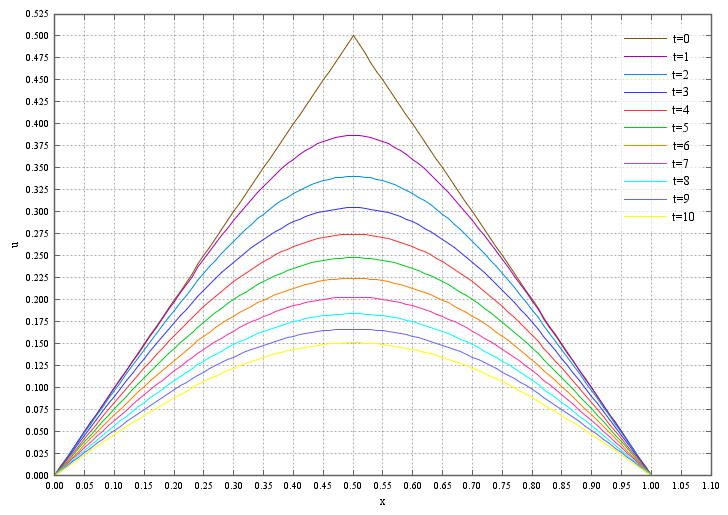
ゆくゆくはこのブログだけで有限要素法やいろいろな語学を学べる、self-contained（必要なものが全てそろった）なものにしていきたいと考えています。なので、記事を読んでいて説明が不足しているなと思われたり、わかりづらいなと思われる箇所がありましたら報せて頂けると幸いです。

離散化の詳細はお待ちください。