2018-11-09

【有限体積法】1次元定常移流拡散方程式を中心差分で解く　C++コード付き

数値計算 Navier-Stokes方程式偏微分方程式数値流体力学数理モデル有限体積法

今回は1次元定常移流拡散方程式を有限体積法（中心差分法）で解いていきます。C++コード付きです。ただし今回は風上化は入れていません。

1次元定常移流拡散方程式とは

$\displaystyle V\frac{du}{dx} -D\frac{d^2u}{dx^2}=0, \quad x \in [0, L]$

のような二階の常微分方程式のことをいいます。ここで、 $u$ は溶質の濃度、 $V$ は風などによる移流速度、 $D$ は拡散の効果を表す拡散係数と解釈することができます。ある溶質が移流や拡散のもとでどのような分布をとるか求めるのがこの問題です。

前回の一次元Poisson方程式に移流を加えます。今境界条件は前回と同じく3パターン用意しました。すなわち、

Case 1, $x=0$ と $x=L$ でDirichlet条件を課す
（ $u(0)$ と $u(L)$ の値を指定）
Case 2, $x=0$ でNeumann条件、 $x=L$ でDirichlet条件を課す
（ $\frac{ \mathrm{d}u }{ \mathrm{d}x }(0)$ と $u(L)$ の値を指定）
Case 3, $x=0$ でDirichlet条件、 $x=L$ でNeumann条件を課す
（ $u(0)$ と $\frac{ \mathrm{d}u }{ \mathrm{d}x }(L)$ の値を指定）

です。それぞれコード上ではbc=1、bc=2、bc=3に対応しています。連立一次方程式の解法はGauss-Seidel法またはTDMAを用いています。好きなほうを選べます。詳しくは以下の記事を参考にして下さい。

コードです。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>

using namespace std;

//Gauss-Seidel//
inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps)
{
	int i,k;
	double in,sum,max;
	for(k=0;k<100000;k++)
	{
		max=0.0;
		in=x[0];
		
		for(i=0;i<Node;i++)
		{
			in=x[i];
			x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i];
			if(max<abs(in-x[i])) max=abs(in-x[i]);
		}
		
		if(eps>max) break;
	}
}

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double D[],double L[],double R[],double b[],double f[], int &Node, double &dx, double &V, double &Diff)
{
	int i;
	for(i=1;i<Node;i++)
	{
		//Diffusion//
		L[i]=-Diff*1.0/dx;
		D[i]=Diff*2.0/dx;
		R[i]=-Diff*1.0/dx;
		
		//Advection//
		L[i]+=-V/2.0;
		R[i]+=V/2.0;
		
		//Source//
		b[i]=-f[i]*dx;
	}
}

inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node, double &dx, double f[], double &V, double &Diff)
{
	if(bc==1)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
	}
	if(bc==2)
	{
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
		D[0]=-V/2.0+Diff*1.0/dx;R[0]=V/2.0-Diff*1.0/dx;b[0]=-f[0]*dx/2.0-N0*Diff;
	}
	if(bc==3)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=-V/2.0-Diff*1.0/dx;D[Node-1]=V/2.0+Diff*1.0/dx;b[Node-1]=-f[Node-1]*dx/2.0+N1*Diff;
	}
}

int main()
{
	int i;
	int Partition=100;
	int Node=Partition+1;//the number of cells is equal to the number of nodes
	double LL=1.0;
	double dx=LL/(Node-1);
	double eps=pow(2.0,-50);
	int bc=1;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=0.0;
	double D1=1.0; 
	double N0=10.0;
	double N1=2.0;
	double Diff=0.01;
	double V=0.1;
	double *b = new double[Node];
	double *x = new double[Node];
	double *f = new double[Node];
	double *D = new double[Node];
	double *L = new double[Node];
	double *R = new double[Node];

	for(i=0;i<Node;i++) 
	{
		b[i]=0.0;x[i]=0.0;f[i]=0.0;D[i]=0.0;L[i]=0.0;R[i]=0.0;
	}
	
	ofstream fk;
	fk.open("answer.txt");
	
	mat(D,L,R,b,f,Node,dx,V,Diff);
	boundary(bc,D0,D1,N0,N1,D,L,R,b,Node,dx,f,V,Diff);
	
	//Gauss-Seidel or TDMA//
	//GS(D,L,R,x,b,Node,eps);
	tdma(D,L,R,b,x,Node);
	
	for(i=0;i<Node;i++) cout<<x[i]<<endl;
	for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl;

	delete[] b,x,f,D,L,R;

	return 0;
}

計算結果を見てみましょう。

f:id:mutsumunemitsutan:20181109233333p:plain:w500

境界条件が正しく反映されていることを確認して下さい。移流の影響で全体的に右に寄っていることがわかります。

こちらの離散化も詳しく書く予定です。中心差分法では移流が卓越する場合をきちんと扱えないので、移流方向を考慮した離散化である風上法などを使う必要があります。

2018-11-08

【有限体積法】1次元Poisson方程式（ポアソン方程式）を有限体積法で解く　C++コード付き

数値計算偏微分方程式数値流体力学数理モデル有限体積法

有限体積法のほうもぼちぼち1次元の場合から解説していきます！

今回は有限体積法の勉強で最初に解くであろう、1次元Poisson方程式を有限要素法（Galerkin法）で解くC++コードを公開します。

普通の有限体積法で離散化します。二次元配列は一次元配列に収納しています。二次元配列を使ったほうが行列を足し合わせるときにわかりやすいので、初心者の方はそれでよいと思います。ただ要素数が増えてくると、二次元配列は重いので一次元配列のみで処理するのがおすすめです。

Poisson方程式とは

$\displaystyle \Delta u+f=0$

のような二階の偏微分方程式のことを言います。ここで $f$ は既知の関数です。1次元の場合は

$\displaystyle \frac{d^2u }{dx^2 }+f=0, \quad x \in [0,L]$

となります。以下では $f=1$ とします。このとき解析解を求めることができます。

境界条件は3パターン扱うことができるようにつくってあります。すなわち、

コードです。今回は行列が三重対角行列になるので、配列のDに対角要素を、Lに対角要素の左隣の要素を、Rに対角要素の右隣の要素を格納しています。

#include <iostream>
#include <cmath>
#include <fstream>
#include <iomanip>

using namespace std;

//Gauss-Seidel//
inline void GS(double D[],double L[],double R[],double x[],double b[], int &Node, double &eps)
{
	int i,k;
	double in,sum,max;
	for(k=0;k<100000;k++)
	{
		max=0.0;
		in=x[0];
		
		for(i=0;i<Node;i++)
		{
			in=x[i];
			x[i]=(b[i]-(L[i]*x[i-1]+R[i]*x[i+1]))/D[i];
			if(max<abs(in-x[i])) max=abs(in-x[i]);
		}
		
		if(eps>max) break;
	}
}

//TDMA//a:diagonal,c:left,b:right,
inline void tdma(double a[], double c[], double b[], double d[], double x[], int size)
{
	int i;
	double *P=new double[size];
	double *Q=new double[size];
	
	//first step//
	P[0]=-b[0]/a[0];
	Q[0]=d[0]/a[0];
	
	//second step//
	for(i=1;i<size;i++)
	{
		P[i]=-b[i]/(a[i]+c[i]*P[i-1]);
		Q[i]=(d[i]-c[i]*Q[i-1])/(a[i]+c[i]*P[i-1]);
	}
	
	//third step, backward//
	x[size-1]=Q[size-1];

	for(i=size-2;i>-1;i=i-1)
	{
		x[i]=P[i]*x[i+1]+Q[i];
	}
	
	delete [] P,Q;
}

inline void mat(double D[],double L[],double R[],double b[],double f[], int &Node, double &dx)
{
	int i;
	for(i=1;i<Node;i++)
	{
		L[i]=1.0/dx;
		D[i]=-2.0/dx;
		R[i]=1.0/dx;
		b[i]=-f[i]*dx;
	}
}

inline void boundary(int &bc,double &D0,double &D1,double &N0,double &N1,double D[],double L[],double R[],double b[],int &Node, double &dx, double f[])
{
	if(bc==1)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
	}
	if(bc==2)
	{
		L[Node-1]=0.0;D[Node-1]=1.0;b[Node-1]=D1;
		D[0]=-1.0/dx;R[0]=1.0/dx;b[0]=-f[0]*dx/2.0+N0;
	}
	if(bc==3)
	{
		D[0]=1.0;R[0]=0.0;b[0]=D0;
		L[Node-1]=1.0/dx;D[Node-1]=-1.0/dx;b[Node-1]=-f[Node-1]*dx/2.0-N1;
	}
}

int main()
{
	int i;
	int Partition=100;
	int Node=Partition+1;//the number of cells is equal to the number of nodes
	double LL=1.0;
	double dx=LL/(Node-1);
	double eps=pow(2.0,-50);
	int bc=3;//bc=1 both Diriclet bc=2 left Neumann bc=3 right Neumann
	double D0=1.0;
	double D1=2.0; 
	double N0=0.0;
	double N1=0.0;
	double *b = new double[Node];
	double *x = new double[Node];
	double *f = new double[Node];
	double *D = new double[Node];
	double *L = new double[Node];
	double *R = new double[Node];

	for(i=0;i<Node;i++) 
	{
		b[i]=0.0;x[i]=0.0;f[i]=1.0;D[i]=0.0;L[i]=0.0;R[i]=0.0;
	}
	
	ofstream fk;
	fk.open("answer.txt");
	
	mat(D,L,R,b,f,Node,dx);
	boundary(bc,D0,D1,N0,N1,D,L,R,b,Node,dx,f);
	
	//Gauss-Seidel or TDMA//
	//GS(D,L,R,x,b,Node,eps);
	tdma(D,L,R,b,x,Node);
	
	for(i=0;i<Node;i++) cout<<x[i]<<endl;
	for(i=0;i<Node;i++) fk<<dx*i<<" "<<x[i]<<endl;

	delete[] b,x,f,D,L,R;

	return 0;
}

コードの流れですが、まず要素の分割数と境界条件の型（bcの値による）を決め、境界条件の設定（値をどうするか）を行い、関数 mat により行列を作成、関数 boundary で境界条件を行列に反映させ、関数 GS（Gauss-Seidel法）またはTDMAで作成した行列を解き、出力しています。出力はテキストファイル "answer.txt" に出てきます。左の行が $x$ 座標で右の行が求めている関数値 $u$ です。

それでは計算結果を見てみましょう。

f:id:mutsumunemitsutan:20181108200958p:plain:w500

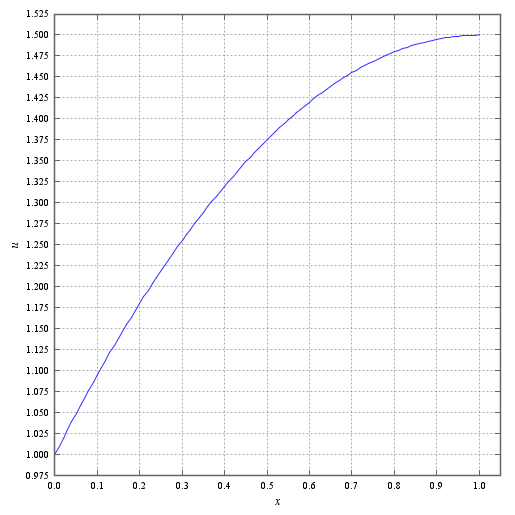
きちんと境界条件が反映されているのがわかるでしょうか。左がDirichlet条件で値は1、右がNeumann条件で値は0です。

今回はコードがメインで離散化の詳細を示していませんが、必ず書くのでお待ちください。

気付いた方がいると思いますが、1次元の場合ほとんどGalerkin法のコードと同じです。主な違いはNeumann境界条件の部分と、行列を組み立てる際に要素ごとではなく、セルごとに行う点です。

2018-10-31

【クラシック】「バッハの無伴奏ヴァイオリンソナタ第1番ト短調 BWV1001」by Henryk Szeryng（シェリング）

クラシック音楽ヴァイオリン

今回はHenryk Szeryngによる「バッハの無伴奏ヴァイオリンソナタ第1番ト短調 BWV1001」です。重厚な響きです。

バッハもシェリングにこんな風に弾いてもらえて満足でしょう。重音と低音が素晴らしい。私はバッハを弾けるほど腕が無いのですが、この重音の弾き方はバッハにぴったりだと思います。

やる気が出ないときはこの演奏をループしています。聞き飽きるということが無いですね。

あとシェリングと言ったら「ヴィターリのシャコンヌ」でしょう。前奏がカットされているのが印象的です。

2018-10-30

【クラシック】「ショパンのノクターン第2番、Op.9-2」by Huberman

クラシック音楽ヴァイオリンピアノ

今回はHubermanによるショパンのノクターン第2番、Op.9-2」です。もとはピアノ独奏曲ですが、これはヴァイオリン編曲版です。

どうでしたか、甘ったるく感じましたか？私にはこれぐらいがちょうどよいです。Kreislerに近い感じがしますね。最近のヴァイオリニストは結構軽やかに弾いてしまうので、HubermanやKreislerの演奏が恋しくなります。例えばドイツのヴァイオリニストDavid Garettです。

「ヴィヴァルディの四季」より夏の第三楽章をヴァイオリンソロで。凄まじい技巧と表現力。間違いなく現代のトッププロの一人。

確かに激しいですが、情念が纏わりつくような重さは皆無です。あくまでさわやかに全てを処理していきます。こういう演奏が聴きたいときもあるので彼も好きです。ただどうしようもないときに元気が出るのはべたべたなHubermanやKreislerの演奏なのです。

Kreisler本人による「愛の悲しみ（Liebesleid、Kreislerによる作曲）」。一音目からポルタメントが甘やか。

2018-10-30

【クラシック】「ポンセのエストレリータ」by ハイフェッツ（Heifetz）

クラシック音楽ヴァイオリン

今回はヴァイオリンの神様、ヤッシャ・ハイフェッツ（Jascha Heifetz）による「ポンセのエストレリータ」です。映画のワンシーンのようですがよく知りません。でもそんなことはどうでもよいくらいよい曲と演奏です。

夜に聴くのがぴたったりなしっとりとした演奏です。ロマンティックな情感で歌いあげます。ハイフェッツは超絶技巧の権化のように思われていますが、彼が真価を発揮するのはエストレリータのような小品を演奏するときなのです！存分に発揮された彼の歌心を聴いて下さい！

2018-10-29

【有限要素法】Cole-Hopf変換による1次元Burgers方程式（バーガース方程式）の解析解

数学有限要素法 Navier-Stokes方程式偏微分方程式数値流体力学数値計算数理モデル

1次元Burgers方程式

$\displaystyle \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}-D \frac{\partial^2 u}{\partial x^2}=0$

の解析解を求めます。『偏微分方程式の数値シミュレーション』のpp.219-220と以下のリンクを参照しています。

偏微分方程式の数値シミュレーション

作者: 登坂宣好,大西和栄
出版社/メーカー: 東京大学出版会
発売日: 1991/04
メディア: 単行本
この商品を含むブログを見る

ステップ1

まず、

$\displaystyle u = \frac{\partial \psi}{\partial x}$

とおきこれを代入すると

$\displaystyle \frac{\partial \psi}{\partial t \partial x}+\frac{\partial \psi}{\partial x} \frac{\partial^2 \psi}{\partial x^2}-D \frac{\partial^3 \psi}{\partial x^3}=0$

を得ます。この第二項目を書きかえると

$\displaystyle \frac{\partial \psi}{\partial t \partial x}+\frac{\partial}{\partial x} \left[ \frac{1}{2} \left( \frac{\partial \psi}{\partial x} \right)^2 \right] -D \frac{\partial^3 \psi}{\partial x^3}=0$

となるので

$\displaystyle \frac{\partial}{\partial x} \left( \frac{\partial \psi}{\partial t}+ \frac{1}{2} \left( \frac{\partial \psi}{\partial x} \right)^2 -D \frac{\partial^2 \psi}{\partial x^2} \right) =0$

を得ます。とりあえず積分定数を0として $x$ で積分して

$\displaystyle \frac{\partial \psi}{\partial t}+ \frac{1}{2} \left( \frac{\partial \psi}{\partial x} \right)^2-D\frac{\partial^2 \psi}{\partial x^2} =0$

となります。

ステップ2

次に

$\displaystyle \psi = -2D \ln \phi$

とおきます。この時点で

$\displaystyle u = \frac{\partial \psi}{\partial x} = -2D\frac{\partial (\ln \phi)}{\partial x} = -2D \frac{\partial}{\partial \phi}(\ln \phi) \frac{\partial \phi}{\partial x} = -2D \frac{1}{\phi}\frac{\partial \phi}{\partial x}$

という変数変換を行ったことになります。これをCole-Hopf変換（コール・ホップ変換）と呼びます。 $\psi$ の偏微分をそれぞれ計算します。

$\displaystyle \frac{\partial \psi}{\partial t} = -2D\frac{\partial}{\partial t} (\ln \phi) = -2D\frac{\partial}{\partial \phi} (\ln \phi)\frac{\partial \phi}{\partial t} = -2D\frac{1}{\phi}\frac{\partial \phi}{\partial t}$

$\displaystyle \frac{\partial \psi}{\partial x} = -2D\frac{\partial}{\partial x} (\ln \phi) = -2D\frac{\partial}{\partial \phi} (\ln \phi)\frac{\partial \phi}{\partial x} = -2D\frac{1}{\phi}\frac{\partial \phi}{\partial x}$

$\displaystyle \begin{eqnarray} \frac{\partial}{\partial x}\left( \frac{\partial \psi}{\partial x} \right) = -2D\frac{\partial}{\partial x}\left( \frac{1}{\phi}\frac{\partial \phi}{\partial x} \right) = -2D\left[ \frac{\partial}{\partial x} \right( \frac{1}{\phi} \left) \frac{\partial \phi}{\partial x} + \frac{1}{\phi}\frac{\partial^2 \phi}{\partial x^2}\right] \\ = -2D\left[ \frac{\partial}{\partial \phi} \right( \frac{1}{\phi} \left) \frac{\partial \phi}{\partial x}\frac{\partial \phi}{\partial x} + \frac{1}{\phi}\frac{\partial^2 \phi}{\partial x^2}\right] = -2D\left[ -\frac{1}{\phi^2} \left( \frac{\partial \phi}{\partial x} \right)^2 + \frac{1}{\phi}\frac{\partial^2 \phi}{\partial x^2}\right] \end{eqnarray}$

これらをステップ1の最後の式に代入します。

$\displaystyle \begin{eqnarray} &&\frac{\partial \psi}{\partial t}+ \frac{1}{2} \left( \frac{\partial \psi}{\partial x} \right)^2-D\frac{\partial^2 \psi}{\partial x^2} \\ &=&-2D\frac{1}{\phi}\frac{\partial \phi}{\partial t} + \frac{1}{2}\left( -2D\frac{1}{\phi}\frac{\partial \phi}{\partial x} \right)^2 +2D^2 \left[ -\frac{1}{\phi^2} \left( \frac{\partial \phi}{\partial x} \right)^2 + \frac{1}{\phi}\frac{\partial^2 \phi}{\partial x^2}\right]\\ &=&-2D\frac{1}{\phi}\frac{\partial \phi}{\partial t} +2D^2 \frac{1}{\phi}\frac{\partial^2 \phi}{\partial x^2}=0 \end{eqnarray}$

すなわち

$\displaystyle \frac{\partial \phi}{\partial t} -D \frac{\partial^2 \phi}{\partial x^2} =0$

と結局、拡散方程式へと変換することができます。拡散方程式はこちらの記事で解説しているフーリエ変換を使う方法によって解くことができます。

この解を用いて1次元Burgers方程式に対する有限要素法（Galerkin法）の精度を調べます。

2018-10-27

【数理モデル】線型反応移流拡散方程式とマルサスモデル（Malthusモデル）

偏微分方程式数学数理モデル

前回1次元Fisher-KPP方程式（フィッシャーKPP方程式）を有限要素法（Galerkin法）で解く話を書いたのですが、そのときに線型反応移流拡散方程式とマルサスモデル（Malthusモデル）の関係について気がつきました。せっかくなので文章として残しておきます。

まず、1次元の線型反応移流拡散方程式は

$\displaystyle \frac{\partial u}{\partial t}+V\frac{\partial u}{\partial x}-D\frac{\partial^2 u}{\partial x^2} +ru=0, \quad x \in [0, L$ ]

のような偏微分方程式です。ここで、 $u(t,x)$ は物質の濃度、 $V$ は流速、 $D$ は物質の広がり具合（拡散）を表す拡散係数、 $r$ が反応により減少する度合いを表す係数と解釈することができます。ここで $r>0$ です。後で説明しますが、偏微分方程式が一本しかないとき、 $r<0$ だと解が発散してしまいます。システムの場合（偏微分方程式が何本かある場合）は必ずしも正でなくてもよかったと思います。初期条件は $f(x)$ で与えます。 $u$ は時間方向と空間方向ともに変化するので二変数関数 $u(t,x)$ となっています。ある物質が移流、拡散、反応のもとどのような分布になるかを表しています。

さて、Fisher-KPP方程式は拡散方程式とLogisticモデルを組み合わせたものと考えることができるのでした。

これと同様にして、線型反応移流拡散方程式は移流拡散方程式とMalthusモデルの組み合わせたものと考えることができます。まず反応項を右辺へ移項します。

$\displaystyle \frac{\partial u}{\partial t}+V\frac{\partial u}{\partial x}-D\frac{\partial^2 u}{\partial x^2} =-ru$

これは移流拡散方程式

$\displaystyle \frac{\partial u}{\partial t}+V\frac{\partial u}{\partial x}-D\frac{\partial^2 u}{\partial x^2} =0$

とMalthusモデル

$\displaystyle \frac{du}{dt} =-ru$

を組み合わせたものです。すなわち移流拡散によって物質の空間的な広がりを、Malthusモデルによって（その場所における、減少するような）物資の反応をあらわしているのです。もし $r<0$ だとすると、 $-r>0$ となり、指数関数的に増大してしまい解が発散してしまいます。なので条件として $r>0$ がついているのです。移流拡散方程式とMalthusモデルの組み合わせと考えるとすっきり理解できます。